题目内容
已知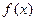 是一次函数,且
是一次函数,且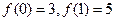 .
.
(1)求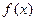 的解析式;
的解析式;
(2)若当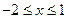 时,函数
时,函数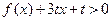 恒成立,求实数
恒成立,求实数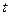 的取值范围
的取值范围
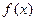 是一次函数,且
是一次函数,且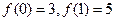 .
.(1)求
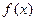 的解析式;
的解析式;(2)若当
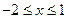 时,函数
时,函数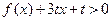 恒成立,求实数
恒成立,求实数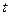 的取值范围
的取值范围(1) (2)
(2)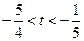
 (2)
(2)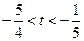
(1) 设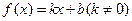 ,由
,由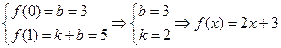 ,
,
(2)由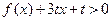 在
在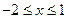 上恒成立,得
上恒成立,得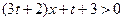 在
在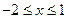 上恒成立,
上恒成立,
令 ,知
,知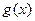 的图象在
的图象在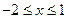 上是一条线段,只需线段的两端点在
上是一条线段,只需线段的两端点在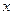 轴的上方,因此要
轴的上方,因此要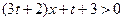 在
在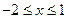 上恒成立,只要:
上恒成立,只要: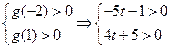 ,
,
得: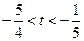 .
.
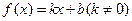 ,由
,由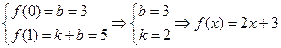 ,
,(2)由
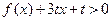 在
在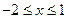 上恒成立,得
上恒成立,得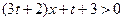 在
在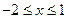 上恒成立,
上恒成立,令
 ,知
,知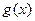 的图象在
的图象在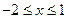 上是一条线段,只需线段的两端点在
上是一条线段,只需线段的两端点在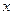 轴的上方,因此要
轴的上方,因此要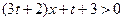 在
在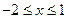 上恒成立,只要:
上恒成立,只要: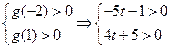 ,
,得:
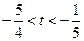 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 。
。 ;
; 。
。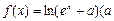 为常数)是实数集R上的奇函数,函数
为常数)是实数集R上的奇函数,函数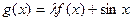 是区间[-1,1]上的减函数.
是区间[-1,1]上的减函数. 上恒成立,求
上恒成立,求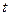 的取值范围;
的取值范围;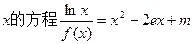 的根的个数.
的根的个数. ,
, ,3].
,3]. ;
; .
.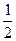 )的值;
)的值;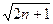 .(2a1-1)·(2a2-1)…(2an-1)对于一切n∈N*均成立?若存在,求出M的范围;若不存在,请说明理由.
.(2a1-1)·(2a2-1)…(2an-1)对于一切n∈N*均成立?若存在,求出M的范围;若不存在,请说明理由.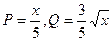 ,今有3万元资金投入经营甲、乙两种商品,为获得最大利润,则对甲、乙两种商品的资金投入分别是多少?能获得最大的利润是多少?
,今有3万元资金投入经营甲、乙两种商品,为获得最大利润,则对甲、乙两种商品的资金投入分别是多少?能获得最大的利润是多少?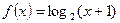 ,当点
,当点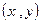 在函数
在函数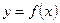 的图象上时,点
的图象上时,点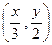 在函数
在函数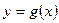 的图象上。
的图象上。 方程的根
方程的根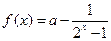 ,(
,(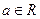 )
)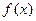 的定义域;
的定义域;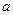 的值;
的值;