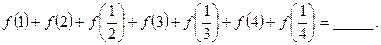题目内容
已知函数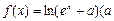
为常数）是实数集R上的奇函数，函数
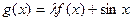是区间[－1，1]上的减函数.
（1）求a的值； （2）若
上恒成立，求
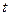的取值范围；
（3）讨论关于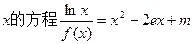
的根的个数.
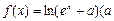为常数）是实数集R上的奇函数，函数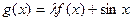是区间[－1，1]上的减函数.（1）求a的值； （2）若
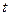上恒成立，求的取值范围；（3）讨论关于
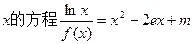的根的个数.（1）a=0；（2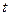）≤－1；（3）①当
时，方程无解.
②当
时，方程有一个根. ③当
时，方程有两个根.
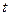≤－1；（3）①当时，方程无解.②当
时，方程有一个根. ③当时，方程有两个根.（1）
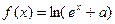是奇函数，则
恒成立.
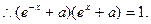即
（2）又
在[－1，1]上单调递减，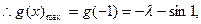
令
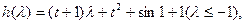则
. （3）由（I）知
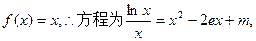
令
，
，当
上为增函数
|
上为减函数，当
时，
而
，
、
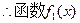在同一坐标系的大致图象如图所示，∴①当
时，方程无解.②当
时，方程有一个根.③当
时，方程有两个根.
练习册系列答案
世纪百通期末金卷系列答案
相关题目
）与时间（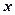
）的函数关系式；
上的最大值为2，求n的取值范围．
+
;
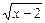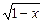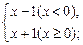④y=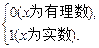
为偶函数且在区间
上是单调增函数．
的解析式；
，若
对任意
恒成立，求实数
的取值范围．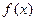
是一次函数，且
.
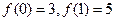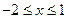时，函数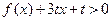
恒成立，求实数
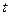的取值范围
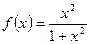，那么