题目内容
.设函数y=f(x)的定义域为(0,+∞),且对任意的正实数x, y,均有
f(xy)=f(x)+f(y)恒成立.已知f(2)=1,且当x>1时,f(x)>0。
(1)求f(1), f(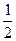 )的值;
)的值;
(2)试判断y=f(x)在(0,+∞)上的单调性,并加以证明;
(3)一个各项均为正数的数列{an}满足f(Sn)=f(an)+f(an+1)-1,n∈N*,其中Sn是数列{an}的前n项和,求数列{an}的通项公式;
(4)在(3)的条件下,是否存在正数M,使2n·a1·a2…an≥M·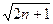 .(2a1-1)·(2a2-1)…(2an-1)对于一切n∈N*均成立?若存在,求出M的范围;若不存在,请说明理由.
.(2a1-1)·(2a2-1)…(2an-1)对于一切n∈N*均成立?若存在,求出M的范围;若不存在,请说明理由.
f(xy)=f(x)+f(y)恒成立.已知f(2)=1,且当x>1时,f(x)>0。
(1)求f(1), f(
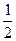 )的值;
)的值;(2)试判断y=f(x)在(0,+∞)上的单调性,并加以证明;
(3)一个各项均为正数的数列{an}满足f(Sn)=f(an)+f(an+1)-1,n∈N*,其中Sn是数列{an}的前n项和,求数列{an}的通项公式;
(4)在(3)的条件下,是否存在正数M,使2n·a1·a2…an≥M·
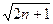 .(2a1-1)·(2a2-1)…(2an-1)对于一切n∈N*均成立?若存在,求出M的范围;若不存在,请说明理由.
.(2a1-1)·(2a2-1)…(2an-1)对于一切n∈N*均成立?若存在,求出M的范围;若不存在,请说明理由.(1)f(1)=0f(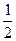 )=-1 (2) 函数y=f(x)在(0,+∞)上是增函数
)=-1 (2) 函数y=f(x)在(0,+∞)上是增函数
(3)数列{an}是首项为1,公差为1的等差数列,从而有an="n "
(4)存在 正数M的范围是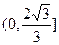
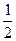 )=-1 (2) 函数y=f(x)在(0,+∞)上是增函数
)=-1 (2) 函数y=f(x)在(0,+∞)上是增函数 (3)数列{an}是首项为1,公差为1的等差数列,从而有an="n "
(4)存在 正数M的范围是
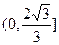
1)∵f(2×1)="f(2)+f(1)," ∴f(1)=0
又∵f(1)=f(2×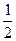 )=f(2)+f(
)=f(2)+f(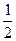 ),且f(2)=1,∴f(
),且f(2)=1,∴f(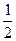 )=-1
)=-1
(2)设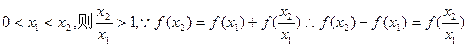 …4分
…4分
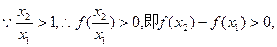
∴函数y=f(x)在(0,+∞)上是增函数
(3)∵f(2)="1," ∴由f(Sn)=f(an)+f(an+1)-1(n∈N*),得f(2Sn)=f[an(an+1)]
∵函数y=f(x)在(0,+∞)上是增函数,
∴2Sn=an(an+1)
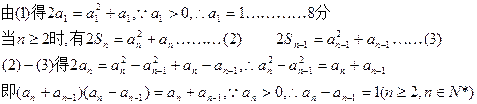
∴数列{an}是首项为1,公差为1的等差数列,从而有an=n
(4)∵an=n,故不等式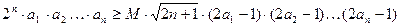
可化为2n×1×2×3×…×n≥M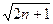 ×1×3×5×…×(2n-1),
×1×3×5×…×(2n-1),
即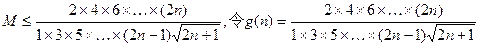
则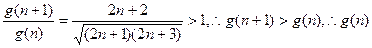 是单调递增
是单调递增
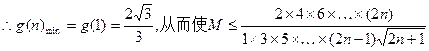 对一切n∈N*都成立的正数M的范围是
对一切n∈N*都成立的正数M的范围是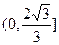
又∵f(1)=f(2×
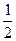 )=f(2)+f(
)=f(2)+f(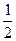 ),且f(2)=1,∴f(
),且f(2)=1,∴f(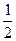 )=-1
)=-1(2)设
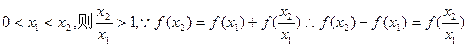 …4分
…4分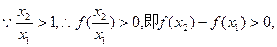
∴函数y=f(x)在(0,+∞)上是增函数
(3)∵f(2)="1," ∴由f(Sn)=f(an)+f(an+1)-1(n∈N*),得f(2Sn)=f[an(an+1)]
∵函数y=f(x)在(0,+∞)上是增函数,
∴2Sn=an(an+1)
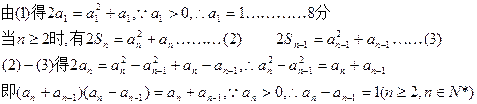
∴数列{an}是首项为1,公差为1的等差数列,从而有an=n
(4)∵an=n,故不等式
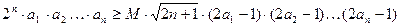
可化为2n×1×2×3×…×n≥M
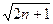 ×1×3×5×…×(2n-1),
×1×3×5×…×(2n-1),即
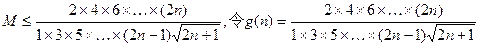
则
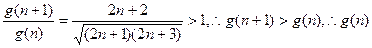 是单调递增
是单调递增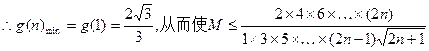 对一切n∈N*都成立的正数M的范围是
对一切n∈N*都成立的正数M的范围是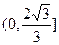

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
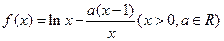 .
.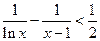 对于
对于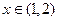 恒成立
恒成立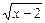 +
+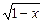 ;
;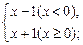 ④y=
④y=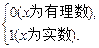
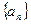 的前
的前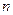 项和
项和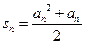 ,
,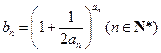 .
.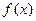 在区间D上是凹函数,且
在区间D上是凹函数,且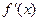 存在,则当
存在,则当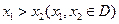 时,总有
时,总有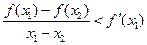 .请根据上述定理,且已知函数
.请根据上述定理,且已知函数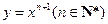 是
是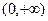 上的凹函数,判断
上的凹函数,判断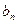 与
与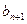 的大小;
的大小;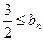 .
.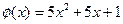
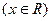 ,函数
,函数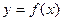 的图象与
的图象与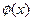 的图象关于点
的图象关于点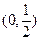 中心对称。
中心对称。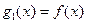 ,
,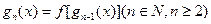 ,试求出使
,试求出使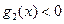 成立的
成立的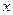 取值范围;
取值范围; ,使
,使 对于区间内的任意实数
对于区间内的任意实数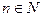 ,且
,且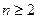 时,都有
时,都有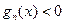 恒成立?
恒成立?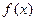 是一次函数,且
是一次函数,且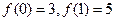 .
.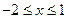 时,函数
时,函数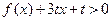 恒成立,求实数
恒成立,求实数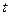 的取值范围
的取值范围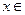
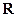 时,一次函数
时,一次函数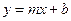 在
在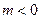 和
和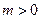 时的单调性是怎样的?利用函数单调性的定义证明你的结论.
时的单调性是怎样的?利用函数单调性的定义证明你的结论.