题目内容
设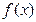 是定义在
是定义在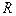 上的奇函数,且
上的奇函数,且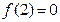 ,则方程
,则方程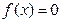 在区间
在区间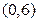 的解的个数的最小值是( )
的解的个数的最小值是( )
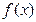 是定义在
是定义在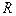 上的奇函数,且
上的奇函数,且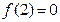 ,则方程
,则方程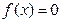 在区间
在区间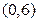 的解的个数的最小值是( )
的解的个数的最小值是( )| A.4 | B.5 | C.6 | D.7 |
C
由题意知,函数的周期是4,因为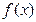 是定义在
是定义在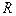 上的奇函数,所以
上的奇函数,所以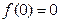 ,则
,则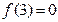 ,
,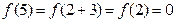 ,
,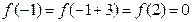 ,
,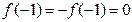 ,
,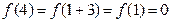 ,
,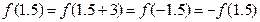 ,所以
,所以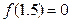 ,
,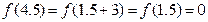 ,故则方程
,故则方程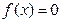 在区间
在区间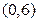 的解的个数的最小值是6.
的解的个数的最小值是6.
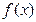 是定义在
是定义在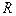 上的奇函数,所以
上的奇函数,所以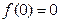 ,则
,则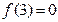 ,
,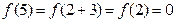 ,
,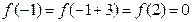 ,
,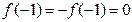 ,
,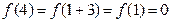 ,
,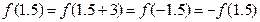 ,所以
,所以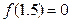 ,
,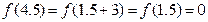 ,故则方程
,故则方程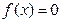 在区间
在区间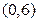 的解的个数的最小值是6.
的解的个数的最小值是6.
练习册系列答案
相关题目
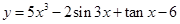 的图象的对称中心是
的图象的对称中心是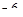 ,0)
,0)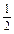 x,求使f(x)=-
x,求使f(x)=-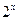 +2x+b(b为常数),则f(-1)=
+2x+b(b为常数),则f(-1)=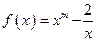 且
且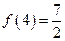 ,
,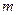 的值;
的值;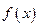 的奇偶性;
的奇偶性;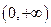 上的单调性,并给予证明.
上的单调性,并给予证明.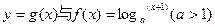 的图象关于原点对称.
的图象关于原点对称.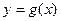 的解析式;
的解析式;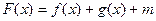 为奇函数,试确定实数m的值;
为奇函数,试确定实数m的值;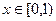 时,总有
时,总有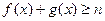 成立,求实数n的取值范围.
成立,求实数n的取值范围.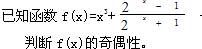
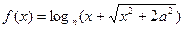 是奇函数,则a= .
是奇函数,则a= .