题目内容
(本小题满分12分)
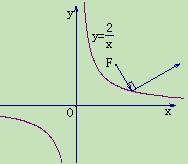
已知F1(-2,0),F2(2,0),点P满足∣PF1∣-∣PF2∣=2,记点P的轨迹为E.
(I)求轨迹E的方程
(II)若直线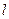 过点F2且与轨迹E交于P,Q两点.无论直线
过点F2且与轨迹E交于P,Q两点.无论直线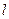 绕点F2怎样转动,在x轴上总存在定点M(m,0),使MP⊥MQ恒成立,求实数m的值.
绕点F2怎样转动,在x轴上总存在定点M(m,0),使MP⊥MQ恒成立,求实数m的值.
已知F1(-2,0),F2(2,0),点P满足∣PF1∣-∣PF2∣=2,记点P的轨迹为E.
(I)求轨迹E的方程
(II)若直线
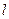 过点F2且与轨迹E交于P,Q两点.无论直线
过点F2且与轨迹E交于P,Q两点.无论直线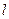 绕点F2怎样转动,在x轴上总存在定点M(m,0),使MP⊥MQ恒成立,求实数m的值.
绕点F2怎样转动,在x轴上总存在定点M(m,0),使MP⊥MQ恒成立,求实数m的值.(Ⅰ)易知轨迹E为双曲线右支,其方程为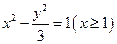 .
.
(Ⅱ)设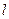 :
: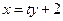 ,代入上式整理得
,代入上式整理得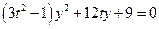 .
.
设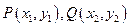 .则有:
.则有:
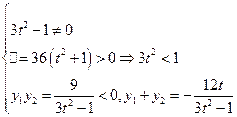
∵
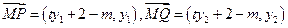 ,且MP⊥MQ.
,且MP⊥MQ.
∴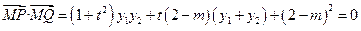
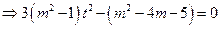 .由题知此式对适合
.由题知此式对适合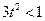 的
的
任意t都成立,故


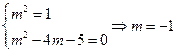 .
.
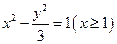 .
.(Ⅱ)设
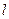 :
: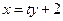 ,代入上式整理得
,代入上式整理得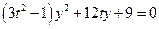 .
.设
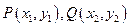 .则有:
.则有: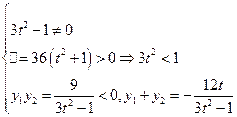
∵

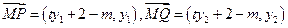 ,且MP⊥MQ.
,且MP⊥MQ.∴
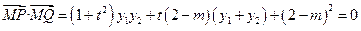
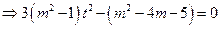 .由题知此式对适合
.由题知此式对适合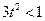 的
的任意t都成立,故


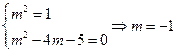 .
.略

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
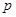 :对任意实数
:对任意实数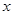 ,不等式
,不等式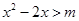 恒成立;命题
恒成立;命题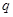 :方程
:方程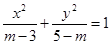 表示焦点在
表示焦点在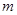 的取值范围;
的取值范围;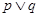 ”为真命题,且“
”为真命题,且“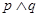 ”为假命题,求实数
”为假命题,求实数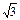 ,D是AB的中点.
,D是AB的中点. ·
·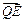 恒为定值时E点的坐标及定值.
恒为定值时E点的坐标及定值. ,直线
,直线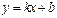 与椭圆
与椭圆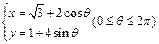 恒有公共点,则
恒有公共点,则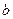 的
的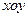 中,设点
中,设点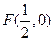 ,直线
,直线 :
: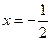 ,点
,点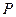 在直线
在直线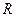 是线段
是线段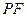 与
与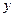 轴的交点,
轴的交点, 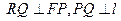 .
.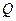 的轨迹的方程
的轨迹的方程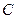 ;
;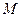 过
过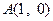 ,且圆心
,且圆心 线
线
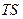 是圆
是圆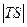 是否为定值?请说明理由.
是否为定值?请说明理由.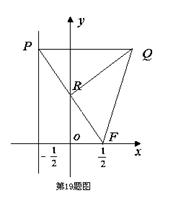
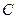 的顶点在原点,焦点F与双曲线
的顶点在原点,焦点F与双曲线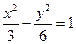 的右焦点重合,过点
的右焦点重合,过点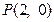 且斜率为1的直线
且斜率为1的直线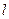 与抛物线
与抛物线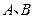 两点
两点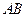 中点到抛物线准线的距离
中点到抛物线准线的距离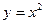 上两点
上两点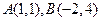 处的切线交于
处的切线交于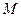 点,则
点,则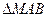 的面积为
的面积为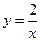 的图像是以直线
的图像是以直线 为轴,以坐标轴为渐近线的等轴双曲线,记作C.
为轴,以坐标轴为渐近线的等轴双曲线,记作C. (2)
(2)