题目内容
【题目】如图所示,四棱锥P﹣ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点. 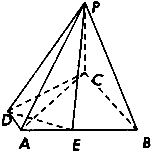
(1)求证:平面PDE⊥平面PAC;
(2)求直线PC与平面PDE所成的角的正弦值.
【答案】
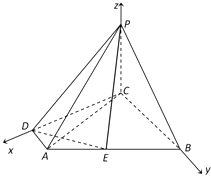
(1)解:以点C为坐标原点,以直线CD,CB,CP分别为x,y,z轴建立空间直角坐标系C﹣xyz,
则C(0,0,0),A(2,1,0),B(0,3,0),P(0,0,2),D(2,0,0),E(1,2,0).
∴ ![]() ,
, ![]() ,
, ![]() ,
,
∴ ![]() ,
, ![]() ,
,
∴DE⊥CA,DE⊥CP,
又CP∩CA=C,AC平面PAC,CP平面PAC,
∴DE⊥平面PAC,∵DE平面PDE,
∴平面PDE⊥平面PAC.
(2)解: ![]() ,
,
设 ![]() 是平面PDE的一个法向量,则
是平面PDE的一个法向量,则 ![]() ,
,
∴ ![]() ,
,
令x=2,则y=1,z=2,即 ![]() ,
,
∴ ![]() =4,|
=4,| ![]() |=3,|
|=3,| ![]() |=2,
|=2,
∴cos< ![]() >=
>= ![]() =
= ![]() .
.
∴直线PC与平面PDE所成的角的正弦值为 ![]() .
.
【解析】(1)点C为坐标原点建立空间直角坐标系,求出向量 ![]() ,
, ![]() ,
, ![]() 的坐标,根据数量积得出DE⊥AC,DE⊥CP,故而DE⊥平面PAC,于是平面PDE⊥平面PAC;(2)求出平面PDE的法向量
的坐标,根据数量积得出DE⊥AC,DE⊥CP,故而DE⊥平面PAC,于是平面PDE⊥平面PAC;(2)求出平面PDE的法向量 ![]() ,计算
,计算 ![]() 与
与 ![]() 的夹角,则直线PC与平面PDE所成的角的正弦值等于|cos<
的夹角,则直线PC与平面PDE所成的角的正弦值等于|cos< ![]() >|.
>|.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目