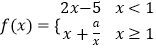题目内容
【题目】记关于x的不等式 
的解集为P，不等式|x+2|＜3的解集为Q
（1）若a=3，求P；
（2）若P∪Q=Q，求正数a的取值范围．
【答案】
（1）解：a=3时， 
即 
，化简得 
∴集合 
，根据分式不等式的解法，解得﹣1＜x＜3
由此可得，集合P=（﹣1，3）
（2）解：Q={x||x+2|＜3}={x|﹣3＜x+2＜3}={x|﹣5＜x＜1}
可得Q=（﹣5，1）
∵a＞0，∴P={ 
}=（﹣1，a），
又∵P∪Q=Q，得PQ，
∴（﹣1，a）（﹣5，1），由此可得0＜a≤1
即正数a的取值范围是（0，1]．
【解析】（1）当a=3时，解分式不等式得到集合P，（2）解绝对值不等式得到集合Q，再通过并集运算得到a的取值范围.
【考点精析】认真审题，首先需要了解绝对值不等式的解法(含绝对值不等式的解法：定义法、平方法、同解变形法，其同解定理有；规律：关键是去掉绝对值的符号)．
练习册系列答案
相关题目
