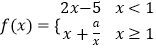题目内容
【题目】某地区的农产品A第x天(1≤x≤20,x∈N*)的销售价格p=50﹣|x﹣6|(元∕百斤),一农户在第x天(1≤x≤20,x∈N*)农产品A的销售量q=a+|x﹣8|(百斤)(a为常数),且该农户在第7天销售农产品A的销售收入为2009元.
(1)求该农户在第10天销售农产品A的销售收入是多少?
(2)这20天中该农户在哪一天的销售收入最大?为多少?
【答案】
(1)解:由已知第7天的销售价格p=50﹣|x﹣6|=50﹣|7﹣6|=49,销售量q=a+|x﹣8|=a+|7﹣8|=a+1.
∴第7天的销售收入W7=pq=49×(a+1)=2009(元).解得,a=40;
所以,第10天的销售收入为W10=p10q10=46×42=1932(元).
(2)解:设第x天的销售收入为Wx,则 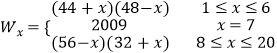 ;
;
当1≤x≤6时, ![]() (当且仅当x=2时取等号),∴当x=2时有最大值W2=2116;
(当且仅当x=2时取等号),∴当x=2时有最大值W2=2116;
当8≤x≤20时, ![]() (当且仅当x=12时取等号),∴当x=12时有最大值W12=1936;
(当且仅当x=12时取等号),∴当x=12时有最大值W12=1936;
由于W2>W7>W12,所以,第2天该农户的销售收入最大.
【解析】(1)第7天的销售价格p=50﹣|x﹣6|=50﹣|7﹣6|=49,销售量q=a+|x﹣8|=a+|7﹣8|=a+1,第7天的销售收入为W7=pq=2009,可得到a=40,(2)设第x天的销售收入为Wx,表示出Wx,在分段函数的各个区间内找到收入最大的值.

练习册系列答案
相关题目