题目内容
18.△ABC的内角A,B,C的对边分别为a,b,c,已知a=2,b=2$\sqrt{3}$,A=$\frac{π}{6}$,则△ABC的面积为( )| A. | $2\sqrt{3}$或$\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $2\sqrt{3}$或$4\sqrt{3}$ | D. | $\sqrt{3}$ |
分析 根据正弦定理和条件求出sinB的值,由内角的范围求出角B的值,由内角和定理和三角形面积公式再求出三角形的面积.
解答 解:由题意知,a=2,b=2$\sqrt{3}$,A=$\frac{π}{6}$,
根据正弦定理得$\frac{a}{sinA}=\frac{b}{sinB}$,则sinB=$\frac{bsinA}{a}$=$\frac{2\sqrt{3}×\frac{1}{2}}{2}$=$\frac{\sqrt{3}}{2}$,
又b>a,则B=$\frac{π}{3}$或$\frac{2π}{3}$,
当B=$\frac{π}{3}$时,C=$π-\frac{π}{6}-\frac{π}{3}$=$\frac{π}{2}$,△ABC的面积S=$\frac{1}{2}×2×2\sqrt{3}$=2$\sqrt{3}$;
当B=$\frac{2π}{3}$时,C=$π-\frac{π}{6}-\frac{2π}{3}$=$\frac{π}{6}$,△ABC的面积S=$\frac{1}{2}absinC$=$\frac{1}{2}×2×2\sqrt{3}×\frac{1}{2}$=$\sqrt{3}$,
综上可得,△ABC的面积是2$\sqrt{3}$或$\sqrt{3}$,
故选:A.
点评 本题考查了正弦、余弦定理,内角和定理,以及三角形的面积公式的应用,属于中档题.

练习册系列答案
相关题目
8.已知集合A=[-4,1),B={0,2},则A∩B为( )
| A. | {0} | B. | {2} | C. | {0,3} | D. | {x|-4<x<1} |
6.某几何体的三视图如图所示,则该几何体的体积为( )
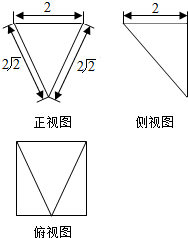

| A. | $\frac{4\sqrt{6}}{3}$ | B. | 2$\sqrt{6}$ | C. | $\frac{4\sqrt{7}}{3}$ | D. | 4$\sqrt{7}$ |
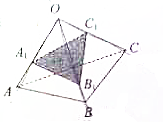 如图,已知三棱锥O-ABC的三条侧棱OA,OB,OC两两垂直,且OA=OC=4,OB=3.
如图,已知三棱锥O-ABC的三条侧棱OA,OB,OC两两垂直,且OA=OC=4,OB=3.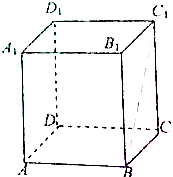 在以棱长为1的正方形ABCD-A1B1C1D1中,求:
在以棱长为1的正方形ABCD-A1B1C1D1中,求: