题目内容
10.平面直角坐标系xOy中,曲线C:$\left\{\begin{array}{l}{x=3cosφ}\\{y=2sinφ}\end{array}\right.$(φ是参数),以平面直角坐标系的原点为极点,x轴的正半轴为极轴建立坐标系.(1)写出曲线C的普通方程并把它化成极坐标方程.
(2)若A、B分别为曲线C上两点,且OA⊥OB,求:$\frac{1}{|OA{|}^{2}}$+$\frac{1}{|OB{|}^{2}}$的值.
分析 (1)消去参数,可得曲线C的普通方程,从而可化成极坐标方程.
(2)设A(ρ1,θ),B(ρ2,θ+$\frac{π}{2}$),利用极坐标方程求:$\frac{1}{|OA{|}^{2}}$+$\frac{1}{|OB{|}^{2}}$的值.
解答 解:(1)曲线C:$\left\{\begin{array}{l}{x=3cosφ}\\{y=2sinφ}\end{array}\right.$(φ是参数),可得曲线C的普通方程$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{4}=1$,
极坐标方程为$\frac{1}{{ρ}^{2}}$=$\frac{co{s}^{2}θ}{9}+\frac{si{n}^{2}θ}{4}$;
(2)设A(ρ1,θ),B(ρ2,θ+$\frac{π}{2}$),
∴$\frac{1}{|OA{|}^{2}}$+$\frac{1}{|OB{|}^{2}}$=$\frac{co{s}^{2}θ}{9}+\frac{si{n}^{2}θ}{4}$+$\frac{co{s}^{2}(θ+\frac{π}{2})}{9}+\frac{si{n}^{2}(θ+\frac{π}{2})}{4}$=$\frac{1}{9}$+$\frac{1}{4}$=$\frac{13}{36}$.
点评 本题考查参数方程与普通方程的互化,考查极坐标方程的运用,考查学生的计算能力,比较基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.△ABC的内角A,B,C的对边分别为a,b,c,已知a=2,b=2$\sqrt{3}$,A=$\frac{π}{6}$,则△ABC的面积为( )
| A. | $2\sqrt{3}$或$\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $2\sqrt{3}$或$4\sqrt{3}$ | D. | $\sqrt{3}$ |
19.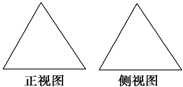 如图是两个全等的正三角形,给出下列三个命题:①存在四棱锥,其正视图、侧视图如图;②存在三棱锥,其正视图、侧视图如图;③存在圆锥,其正视图、侧视图如图.其中所有真命题的序号是( )
如图是两个全等的正三角形,给出下列三个命题:①存在四棱锥,其正视图、侧视图如图;②存在三棱锥,其正视图、侧视图如图;③存在圆锥,其正视图、侧视图如图.其中所有真命题的序号是( )
 如图是两个全等的正三角形,给出下列三个命题:①存在四棱锥,其正视图、侧视图如图;②存在三棱锥,其正视图、侧视图如图;③存在圆锥,其正视图、侧视图如图.其中所有真命题的序号是( )
如图是两个全等的正三角形,给出下列三个命题:①存在四棱锥,其正视图、侧视图如图;②存在三棱锥,其正视图、侧视图如图;③存在圆锥,其正视图、侧视图如图.其中所有真命题的序号是( )| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
20.在平面直角坐标系xOy中,双曲线中心在原点,焦点在y轴上,一条渐近线方程为x-3y=0,则它的离心率为( )
| A. | $\sqrt{5}$ | B. | $\sqrt{10}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{2}$ |
