题目内容
18.已知等比数列{an}中,a2=$\frac{1}{3}$,公比q=$\frac{1}{3}$,Sn为{an}的前n项和.(1)求an和Sn
(2)设bn=log3a1+log3a2+…+log3an,求数列bn的通项公式.
分析 (1)由已知条件利用等比数列的性质求出首项和公比,由此能求出an和Sn.
(2)利用等比数列的通项公式和对数的运算法则,结合等比数列、等差数列的性质能求出数列{bn}的通项公式.
解答 解:(1)∵等比数列{an}中,a2=$\frac{1}{3}$,公比q=$\frac{1}{3}$,Sn为{an}的前n项和.
∴${a}_{1}=\frac{\frac{1}{3}}{\frac{1}{3}}$=1,
∴an=${a}_{1}{q}^{n-1}$=${({\frac{1}{3}})^{n-1}}$,
Sn=$\frac{{a}_{1}(1-{q}^{n})}{1-q}$=$\frac{1-\frac{1}{{3}^{n}}}{1-\frac{1}{3}}$=$\frac{3}{2}-\frac{3}{2}{(\frac{1}{3})^n}$.
(Ⅱ)bn=log3a1+log3a2+…+log3an
=$lo{g}_{3}[1×(\frac{1}{3})×(\frac{1}{3})^{2}×…×(\frac{1}{3})^{n-1}]$
=$lo{g}_{3}[(\frac{1}{3})^{1+2+…+n-1}]$
=$lo{g}_{3}{3}^{-\frac{(n-1)(1+n-1)}{2}}$
=$-\frac{n(n-1)}{2}$.
∴bn=-$\frac{n(n-1)}{2}$.
点评 本题考查数列的通项公式、前n项和公式的求法,是中档题,解题时要认真审题,注意等差数列、等比数列的性质、对数函数的运算法则的合理运用.

练习册系列答案
相关题目
9.已知函数f(x)=$\frac{1+lnx}{x}$在区间(a,a+$\frac{2}{3}$)(a>0)上存在极值,则实数a的取值范围是( )
| A. | (0,1) | B. | ($\frac{1}{3}$,1) | C. | ($\frac{1}{2}$,1) | D. | ($\frac{2}{3}$,1) |
6.如果实数x,y满足x2+y2=4,那么$\frac{y-2}{x+3}$的最小值是( )
| A. | -$\frac{12}{5}$ | B. | -1 | C. | -$\frac{5}{12}$ | D. | 0 |
7.已知$a={log_3}\frac{1}{2},b={2^{0.01}},c=ln\frac{1}{2}$,则a,b,c的大小关系为( )
| A. | b>a>c | B. | b>c>a | C. | a>c>b | D. | a>b>c |
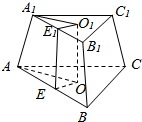 正三棱台的高为3,上、下底面边长分别为2和4,求这个棱台的侧棱长和斜高.
正三棱台的高为3,上、下底面边长分别为2和4,求这个棱台的侧棱长和斜高.