╠Ô─┐─┌╚¦
ÊÐͬ¿ÁÒF1ú¿-
ú¼0ú®ú¼F2ú¿
ú¼0ú®ú¼Â»ÁÒRÈ┌÷¤▀C╔¤È╦»ÃÊ▒ú│Í|RF1|+|RF2|Á─ÍÁ▓╗▒õú¼Ã·¤▀C╣²ÁÒTú¿0ú¼1ú®ú¼
ú¿ó±ú®Ã¾Ã·¤▀CÁ─À¢│╠ú╗
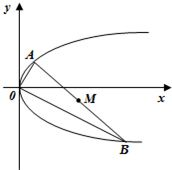
ú¿ó‗ú®M╩Ã÷¤▀C╔¤Ê╗ÁÒú¼╣²ÁÒMθð▒┬╩ÀÍ▒╬¬k1║═k2Á─Í▒¤▀MAú¼MB¢╗÷¤▀CË┌AíóB┴¢ÁÒú¼╚¶AíóB╣ÏË┌È¡ÁÒÂÈ│ãú¼Ã¾k1•k2Á─ÍÁú╗
ú¿ó¾ú®Í▒¤▀l╣²ÁÒF2ú¼ÃÊËÙ÷¤▀C¢╗Ë┌PQú¼Ëð╚þ¤┬├³╠Ôpú║í░Á▒Í▒¤▀l┤╣Í▒Ë┌xÍß╩▒ú¼í¸F1PQÁ─├µ╗²╚íÁ├ί┤¾ÍÁí▒ú«┼ð¤├³╠ÔpÁ─ıµ╝┘ú«╚¶╩Ãıµ├³╠Ôú¼ÃÙ©°ËÞÍñ├¸ú╗╚¶╩Ã╝┘├³╠Ôú¼ÃÙ╦Á├¸└ÝË╔ú«
| 3 |
| 3 |
ú¿ó±ú®Ã¾Ã·¤▀CÁ─À¢│╠ú╗
ú¿ó‗ú®M╩Ã÷¤▀C╔¤Ê╗ÁÒú¼╣²ÁÒMθð▒┬╩ÀÍ▒╬¬k1║═k2Á─Í▒¤▀MAú¼MB¢╗÷¤▀CË┌AíóB┴¢ÁÒú¼╚¶AíóB╣ÏË┌È¡ÁÒÂÈ│ãú¼Ã¾k1•k2Á─ÍÁú╗
ú¿ó¾ú®Í▒¤▀l╣²ÁÒF2ú¼ÃÊËÙ÷¤▀C¢╗Ë┌PQú¼Ëð╚þ¤┬├³╠Ôpú║í░Á▒Í▒¤▀l┤╣Í▒Ë┌xÍß╩▒ú¼í¸F1PQÁ─├µ╗²╚íÁ├ί┤¾ÍÁí▒ú«┼ð¤├³╠ÔpÁ─ıµ╝┘ú«╚¶╩Ãıµ├³╠Ôú¼ÃÙ©°ËÞÍñ├¸ú╗╚¶╩Ã╝┘├³╠Ôú¼ÃÙ╦Á├¸└ÝË╔ú«
ú¿ó±ú®í▀|RF1|+|RF2|=|TF1|+|TF2|=2
=4ú¥|F1F2|=2
ú¼
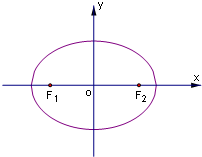
íÓ÷¤▀C╬¬ÊÈÈ¡ÁÒ╬¬Íðð─ú¼F1íóF2╬¬¢╣ÁÒÁ─═ÍÈ▓ú¼
╔Þãõ░Ù│ñÍß╬¬aú¼░ÙÂ╠Íß╬¬bú¼░Ù¢╣¥Ó╬¬cú¼È‗2a=2ú¼2c=2
ú¼
íÓa=2ú¼c=
ú¼b2=a2-c2=1ú«
íÓ÷¤▀CÁ─À¢│╠╬¬
+y2=1ú╗
ú¿ó‗ú®╔ÞMú¿x0ú¼y0ú®ú¼Aú¿x1ú¼y1ú®È‗Bú¿-x1ú¼-y1ú®ú¼
í▀ÁÒMú¼AÈ┌═ÍÈ▓
+y2=1╔¤ú¼
íÓ
+y02=1ú¼
+y12=1ú¼
¤Ó╝§Á├
+y02-y12=0ú¼
ËÍk1=
ú¼k2=
ú¼
íÓk1•k2=
=-
ú╗
ú¿ó¾ú®╔ÞÍ▒¤▀lÁ─À¢│╠╬¬x=my+
ú¼┤·╚Ù═ÍÈ▓À¢│╠
+y2=1ú¼
Á├(4+m2)y2+2
my-1=0ú¼╝ã╦Ò▓ó┼ð¤Á├í¸ú¥0ú¼
╔ÞPú¿x3ú¼y3ú®ú¼Qú¿x4ú¼y4ú®ú¼Á├
ú¼
íÓ|PQ|=
=
=
ú«
F1Á¢Í▒¤▀lÁ─¥Ó└Ùd=
ú¼
╔Þt=
ú¼È‗tí¦1ú¼
íÓSí¸F1PQ=
|PQ|•d=4
í┴
=
=
í▄2ú«
Á▒t2=3ú¼╝┤m2=2ú¼m=í└
╩▒ú¼í¸F1PQÁ─├µ╗²Î¯┤¾ú«
íÓÈ¡├³╠Ô╩Ã╝┘├³╠Ôú¼í¸F1PQÁ─├µ╗²╚íÁ├ί┤¾ÍÁ╩▒ú¼Í▒¤▀lÁ─À¢│╠╬¬ú║
x+
y-
=0║═x-
y-
=0ú«
(
|
| 3 |
íÓ÷¤▀C╬¬ÊÈÈ¡ÁÒ╬¬Íðð─ú¼F1íóF2╬¬¢╣ÁÒÁ─═ÍÈ▓ú¼
╔Þãõ░Ù│ñÍß╬¬aú¼░ÙÂ╠Íß╬¬bú¼░Ù¢╣¥Ó╬¬cú¼È‗2a=2ú¼2c=2
| 3 |
íÓa=2ú¼c=
| 3 |
íÓ÷¤▀CÁ─À¢│╠╬¬
| x2 |
| 4 |
ú¿ó‗ú®╔ÞMú¿x0ú¼y0ú®ú¼Aú¿x1ú¼y1ú®È‗Bú¿-x1ú¼-y1ú®ú¼
í▀ÁÒMú¼AÈ┌═ÍÈ▓
| x2 |
| 4 |
íÓ
| x02 |
| 4 |
| x12 |
| 4 |
¤Ó╝§Á├
| x02-x12 |
| 4 |
ËÍk1=
| y0-y1 |
| x0-x1 |
| y0+y1 |
| x0+x1 |
íÓk1•k2=
| y02-y12 |
| x02-x12 |
| 1 |
| 4 |
ú¿ó¾ú®╔ÞÍ▒¤▀lÁ─À¢│╠╬¬x=my+
| 3 |
| x2 |
| 4 |
Á├(4+m2)y2+2
| 3 |
╔ÞPú¿x3ú¼y3ú®ú¼Qú¿x4ú¼y4ú®ú¼Á├
|
íÓ|PQ|=
| (x3-x4)2+(y3-y4)2 |
| (1+m2)[(y3+y4)2-4y3y4] |
=
| 4(1+m2) |
| 4+m2 |
F1Á¢Í▒¤▀lÁ─¥Ó└Ùd=
2
| ||
|
╔Þt=
| 1+m2 |
íÓSí¸F1PQ=
| 1 |
| 2 |
| 3 |
| ||
| 4+m2 |
=
4
| ||
| t2+3 |
4
| ||
t+
|
Á▒t2=3ú¼╝┤m2=2ú¼m=í└
| 2 |
íÓÈ¡├³╠Ô╩Ã╝┘├³╠Ôú¼í¸F1PQÁ─├µ╗²╚íÁ├ί┤¾ÍÁ╩▒ú¼Í▒¤▀lÁ─À¢│╠╬¬ú║
x+
| 2 |
| 3 |
| 2 |
| 3 |

┴À¤░▓ߤÁ┴ð┤░©
¤Ó╣Ï╠Ô─┐