题目内容
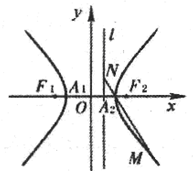
如图,A1、A2、F1、F2分别是双曲线C:
-
=1的左、右顶点和左、右焦点,M(x0、y0)是双曲线C上任意一点,直线MA2与动直线l:x=
相交于点N.
(1)求点N的轨迹E的方程;
(2)点B为曲线E上第一象限内的一点,连接F1B交曲线E于另一点D,记四边形A1A2BD对角线的交点为G,证明:点G在定直线上.
| x2 |
| 9 |
| y2 |
| 16 |
| 9 |
| x0 |
(1)求点N的轨迹E的方程;
(2)点B为曲线E上第一象限内的一点,连接F1B交曲线E于另一点D,记四边形A1A2BD对角线的交点为G,证明:点G在定直线上.

(本小题满分13分)
(1)直线MA2方程为:y0(x-3)-(x0-3)y=0
由方程组
…(2分)
代入双曲线方程化简得:
点N的轨迹E的方程为:
+
=1…(5分)
(2)证明:如图,设B(3cosθ,4sinθ)(0<θ<
),
则直线F1B的方程为:y=
(x+5)
代入E的方程化简得:
(17+15cosθ)x2+(45sin2θ)x-9cosθ(17cosθ+15)=0…(9分)
∴xD=-
=-
,
yD=
,
∴A1B的方程为:4sinθ(x+3)-3(cosθ+1)y=0①
A2D的方程为:sinθ(x-3)+3(cosθ+1)y=0②…(11分)
由①②消去y得:x=-
即点G在双曲线C的左准线x=-
上.…(13分)
(1)直线MA2方程为:y0(x-3)-(x0-3)y=0
由方程组
|

代入双曲线方程化简得:
点N的轨迹E的方程为:
| y2 |
| 16 |
| x2 |
| 9 |
(2)证明:如图,设B(3cosθ,4sinθ)(0<θ<
| π |
| 2 |
则直线F1B的方程为:y=
| 4sinθ |
| 3cosθ+5 |
代入E的方程化简得:
(17+15cosθ)x2+(45sin2θ)x-9cosθ(17cosθ+15)=0…(9分)
∴xD=-
| 9cosθ(17cosθ+15) |
| xB(17+15cosθ) |
| 3(17cosθ+15) |
| 17+15cosθ |
yD=
| 32sinθ |
| 17+15cosθ |
∴A1B的方程为:4sinθ(x+3)-3(cosθ+1)y=0①
A2D的方程为:sinθ(x-3)+3(cosθ+1)y=0②…(11分)
由①②消去y得:x=-
| 9 |
| 5 |
即点G在双曲线C的左准线x=-
| 9 |
| 5 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 O,过BC中点D作平行于AC的直线l,l交AB于E,交
O,过BC中点D作平行于AC的直线l,l交AB于E,交