Question

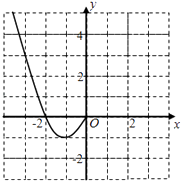
【题目】已知函数，

（1）求函数的图象在点处的切线方程；

（2）当时，求证：；

（3）若对任意的恒成立，求实数的取值范围.

Answer 1

【答案】（1）y=x（2）见解析（3）(-∞,e-2)

【解析】试题分析：

(1)首先求得切线的斜率为1，然后利用点斜式方程可得函数的图象在点处的切线方程是y=x；

(2)构造新函数g(x)= f(x)+x2-x= ex-x-1，由g(x)min= g(0)=0即可证得题中的结论；

(3)分离系数，构造新函数，结合恒成立的条件可得实数的取值范围是(-∞,e-2)

试题解析：

(1) ,所以，切点为(0,0) ∴切线为y=x

(2)证明：令g(x)= f(x)+x2-x= ex-x-1 ,g(x)= ex-1=0 ∴x=0

所以x (-∞，0)时，g(x)<0, g(x)单调递减.x(0，+∞)时，g(x)>0, g(x)单调递增

∴g(x)min= g(0)=0 ∴g(x) 0 ∴f(x) -x2+x

(3) f(x) kx对任意的x (0,+ ∞)恒成立等价于k<对任意的x(0,+ ∞)恒成立

令h(x)=, ∴h(x)=由(2)知x(0,+ ∞)时ex-x-1>0

∴x(0,1)时&#xF06A;&#xF0A2;h(x)<0, (xspan>)单调递减，x(1,+ ∞)时&#xF06A;&#xF0A2;h(x)>0, h(x)单调递增

∴h(x)min=h(1)=e-2 ∴k<e-2 ∴k的取值范围(-∞,e-2)