Question

【题目】已知函数f（x）=log （x2﹣ax+b）． （Ⅰ）若函数f（x）的定义域为（﹣∞，2）∪（3，+∞），求实数a，b的值；
（Ⅱ）若f（﹣2）=﹣3且f（x）在（﹣∞，﹣1]上为增函数，求实数b的取值范围．

Answer 1

【答案】解：（Ⅰ）由题意，不等式x2﹣ax+b＞0 的解集是 （﹣∞，2）∪（3，+∞）， 所以2，3是方程x2﹣ax+b=0 的两实根，
∴2+3=a且2×3=b，
即a=5，b=6
（Ⅱ）设g（x）=x2﹣ax+b，
由f（﹣2）=﹣3得g（﹣2）=4+2a+b=8，
即a= （4﹣b）
又 f（x）在（﹣∞，﹣1]上为增函数，
所以g（x）=x2﹣ax+b在（﹣∞，﹣1]上是减函数且恒为正数，
∴ ，
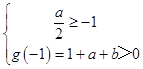也即 ，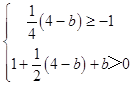
解得：b∈（﹣6，8]
【解析】（Ⅰ）由题意，不等式x2﹣ax+b＞0 的解集是 （﹣∞，2）∪（3，+∞），所以2，3是方程x2﹣ax+b=0 的两实根，由韦达定理，可得实数a，b的值；（Ⅱ） 设g（x）=x2﹣ax+b，若f（﹣2）=﹣3且f（x）在（﹣∞，﹣1]上为增函数，则g（﹣2）=8，g（x）=x2﹣ax+b在（﹣∞，﹣1]上是减函数且恒为正数，进而可得实数b的取值范围．
【考点精析】本题主要考查了二次函数的性质的相关知识点，需要掌握当时，抛物线开口向上，函数在上递减，在上递增；当时，抛物线开口向下，函数在上递增，在上递减才能正确解答此题．