题目内容
13．定义在R上的函数f（x）满足：对于任意x，都有f（x）=f（x-1）+f（x+1），则f（x）的一个周期为6．分析 由已知中f（x）=f（x-1）+f（x+1），可得f（x+6）=f（x），进而得到答案．
解答 解：∵定义在R上的函数f（x）满足：对于任意x，都有f（x）=f（x-1）+f（x+1），
用x-1替换x，可得：f（x-1）=f（x-2）+f（x），
故f（x+1）=-f（x-2），
∴f（x+6）=f[（x+5）+1）=-f[（x+5）-2]=-f（x+3）=-f[（x+2）+1）=f[（x+2）-2]=f（x），
故f（x）的一个周期为6，
故答案为：6
点评 本题考查的知识点是函数的周期性，根据已知得到f（x+6）=f（x），是解答的关键．
练习册系列答案
相关题目
3．经过点A（$\sqrt{3}$，-1），且倾斜角为60°的直线方程为（ ）
| A． | $\sqrt{3}$x-y-4=0 | B． | $\sqrt{3}$x+y-2=0 | C． | $\sqrt{3}$x-y-2=0 | D． | $\sqrt{3}$x+y-4=0 |
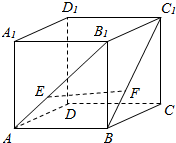如图，正方体ABCD-A1B1C1D1，E，F分别在AB1，BC1上，且$\frac{{B}_{1}E}{AE}$=$\frac{{C}_{1}F}{BF}$=2，过EF做一个平面和面ABCD相交，并找到交线，写出作法．（注意：交线必须是由两个确定的点的连线）
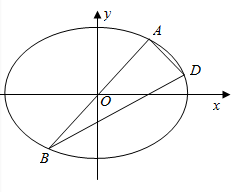如图，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），离心率为$\frac{1}{2}$．过原点的直线与椭圆C交于A、B两点（A，B不是椭圆C的顶点），点D在椭圆C上，且AD⊥AB．
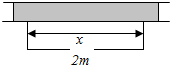围建一个面积为360m2的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需要维修），其他三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，已知旧墙的维修费用为45元/m，新墙的造价为180元/m，设利用的旧墙的长度为x（单位：米），修建此矩形场地围墙的总费用为y（单位：元）．