��Ŀ����
8��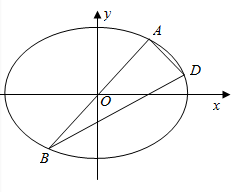 ��ͼ����֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{1}{2}$����ԭ���ֱ������ԲC����A��B���㣨A��B������ԲC�Ķ��㣩����D����ԲC�ϣ���AD��AB��
��ͼ����֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{1}{2}$����ԭ���ֱ������ԲC����A��B���㣨A��B������ԲC�Ķ��㣩����D����ԲC�ϣ���AD��AB����1������ԲC�����߷���Ϊ��x=4������ԲC�ķ��̣�
��2����ֱ��BD��AB��б�ʷֱ�Ϊk1��k2����$\frac{{k}_{1}}{{k}_{2}}$��ֵ��
���� ��1��������Բ�������ʹ�ʽ���߷��̣���a��b��c�Ĺ�ϵ���ⷽ�̿ɵ�a��b�������õ���Բ���̣�
��2����A��x1��y1����x1y1��0����D��x2��y2������B��-x1��-y1��������ֱ�ߵ�б�ʹ�ʽ������ֱ�ߴ�ֱ���������ɵ�AD��б�ʣ���ֱ��AD�ķ���Ϊy=kx+m��k��m��0����������Բ���̣���Τ�ﶨ�������ֱ�ߵ�б�ʹ�ʽ�ɵ�BD��б�ʣ������õ�����ֵ��
��� �⣺��1��������Ϊ$\frac{1}{2}$����Ϊe=$\frac{c}{a}$=$\frac{1}{2}$��
���߷���Ϊ��x=4����Ϊ$\frac{{a}^{2}}{c}$=4��
��b2=a2-c2���ⷽ�̿ɵ�a=2��b=$\sqrt{3}$��
����Բ�ķ���Ϊ$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1��
��2����A��x1��y1����x1y1��0����D��x2��y2������B��-x1��-y1����
��kAB=$\frac{{y}_{1}}{{x}_{1}}$��AD��AB����ֱ��AD��б��k=-$\frac{{x}_{1}}{{y}_{1}}$��
��ֱ��AD�ķ���Ϊy=kx+m��k��m��0����������Բ���̣�
��ȥy�����ã���b2+a2k2��x2+2ma2k2x+a2m2-a2b2=0��
��Τ�ﶨ����֪��x1+x2=-$\frac{2m{a}^{2}{k}^{2}}{{b}^{2}+{a}^{2}{k}^{2}}$��
��y1+y2=k��x1+x2��+2m=$\frac{2m{b}^{2}}{{b}^{2}+{a}^{2}{k}^{2}}$��
�����֪��x1��-x2����k1=$\frac{{y}_{1}+{y}_{2}}{{x}_{1}+{x}_{2}}$=-$\frac{{b}^{2}}{-k{a}^{2}}$=$\frac{{b}^{2}}{{a}^{2}}$•$\frac{{y}_{1}}{{x}_{1}}$=$\frac{{b}^{2}}{{a}^{2}}$k2��
����$\frac{{k}_{1}}{{k}_{2}}$��ֵΪ$\frac{{b}^{2}}{{a}^{2}}$��
��e=$\frac{c}{a}$=$\frac{1}{2}$���ɵ�$\frac{{a}^{2}-{b}^{2}}{{a}^{2}}$=$\frac{1}{4}$��
��$\frac{{b}^{2}}{{a}^{2}}$=$\frac{3}{4}$��
����$\frac{{k}_{1}}{{k}_{2}}$��ֵ$\frac{3}{4}$��
���� ������һ��ֱ������Բ���ۺ��⣬������Բ���̵����Լ���Բ�����ʣ��������������ע����ⷽ���Ļ��ۣ������е���

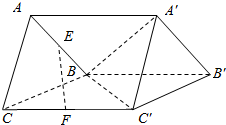 ��ͼ��������ABC-A��B��C�䣬E��F�ֱ���AB��CC����е㣬��EF��һ��ƽ�����A��BC���ཻ�����ҵ����ߣ�д����������ע�⣺���߱�����������ȷ���ĵ�����ߣ�
��ͼ��������ABC-A��B��C�䣬E��F�ֱ���AB��CC����е㣬��EF��һ��ƽ�����A��BC���ཻ�����ҵ����ߣ�д����������ע�⣺���߱�����������ȷ���ĵ�����ߣ�