题目内容
【题目】已知奇函数f（x）是定义在（﹣2，2）上的减函数，则不等式f（ 
）+f（2x﹣1）＞0的解集是（ ）
A.（﹣∞， 
）
B.[﹣ 
，+∞）
C.（﹣6，﹣ ）
D.（﹣ ， ）
【答案】D
【解析】解：f（x）是奇函数，
所以不等式f（ 
）+f（2x﹣1）＞0等价于
f（ ）＞﹣f（2x﹣1）=f（1﹣2x），
又f（x）是定义在（﹣2，2）上的减函数，
所以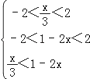 
，
即 
，
解得﹣ 
＜x＜ 
，
则不等式的解集为（﹣ ， ）．
故选：D．
【考点精析】本题主要考查了函数单调性的判断方法的相关知识点，需要掌握单调性的判定法：①设x1,x2是所研究区间内任两个自变量，且x1＜x2；②判定f(x1)与f(x2)的大小；③作差比较或作商比较才能正确解答此题．
练习册系列答案
相关题目
【题目】某厂生产甲、乙两种产品每吨所需的煤、电和产值如下表所示．
用煤（吨） | 用电（千瓦） | 产值（万元） | |
甲产品 | 3 | 50 | 12 |
乙产品 | 7 | 20 | 8 |
但国家每天分配给该厂的煤、电有限，每天供煤至多47吨，供电至多300千瓦，问该厂如何安排生产，使得该厂日产值最大？最大日产值为多少？
