题目内容
【题目】已知A、B是抛物线W： 
上的两个动点，F是抛物线W的焦点， 
是坐标原点，且恒有
.
(1)若直线OA的倾斜角为
时，求线段AB的中点C的坐标；
(2)求证直线AB经过一定点，并求出此定点.
【答案】（1）中点C（
）（2）定点坐标
【解析】试题分析:(1)由点斜式写出直线OA 方程,与抛物线方程联立解得A点坐标，由
得直线OB的倾斜角为
，由点斜式写出直线OB方程,与抛物线方程联立解得B点坐标，最后根据中点坐标公式得 AB的中点C的坐标；(2)先设直线OA的斜率，由点斜式写出直线OA 方程,与抛物线方程联立解得A点坐标，由
得直线OB的斜率，由点斜式写出直线OB方程,与抛物线方程联立解得B点坐标，根据两点式得AB方程，根据方程求出定点坐标
试题解析:（1）OA: 
,所以由
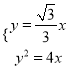得
因为
，所以OB: 
,所以由
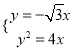得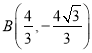
因此线段AB的中点C的坐标为（
）
（2）设OA: 
,所以由
得
因为
，所以OB: 
,所以由
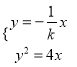得
所以AB: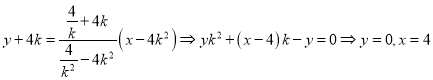 
因此直线AB经过一定点
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
【题目】某企业节能降耗技术改造后，在生产某产品过程中几录的产量x（吨）与相应的生产能耗y（吨）的几 组对应数据如表所示：
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | a |
若根据表中数据得出y关于x的线性回归方程为 
=0.7x+0.35，则表中a的值为（ ）
A.3
B.3.15
C.3.5
D.4.5
