题目内容
【题目】如图,在矩形ABCD中,AB=2BC,点M在边DC上,点F在边AB上,且DF⊥AM,垂足为E,若将△ADM沿AM折起,使点D位于D′位置,连接D′B,D′C得四棱锥D′﹣ABCM. 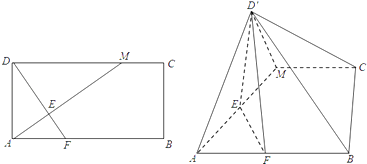
(1)求证:AM⊥D′F;
(2)若∠D′EF= ![]() ,直线D'F与平面ABCM所成角的大小为
,直线D'F与平面ABCM所成角的大小为 ![]() ,求直线AD′与平面ABCM所成角的正弦值.
,求直线AD′与平面ABCM所成角的正弦值.
【答案】
(1)证明:∵AM⊥D′E,AM⊥EF,D′E∩⊥EF=E,
∴AM⊥面D′EF
∵D′F面D′EF,
∴AM⊥D′F;
(2)解:由(1)知,AM⊥面D′EF,AM平面ABCM,
∴平面ABCM⊥面D′EF,
∴过D′作D′H⊥EF,则D′H⊥平面ABCM,
∴∠D′FH也就是∠D′FE是直线D'F与平面ABCM所成角,由已知,∠D′FE= ![]() ,
,
并且∠D′AH是所求的直线AD′与平面ABCM所成角.
∵∠D′EF= ![]() ,且∠D′FE=
,且∠D′FE= ![]()
在三角形△D′EF中,∵∠D′EF= ![]() ,且∠D′FE=
,且∠D′FE= ![]()
所以是等边三角形,∴D′E=EF,即DE=EF,∴△DAF是等腰三角形.
设AD=2,∴AF=2,EF= ![]() ,四棱锥D′﹣ABCM的高D′H=
,四棱锥D′﹣ABCM的高D′H= ![]()
由于直线AD′与平面ABCM所成角为∠D′AH,∴sin∠D′AH= ![]() =
= ![]()

【解析】(1)根据图形折叠前后的关系,易证AM⊥面D′EF,得出AM⊥D′F.(2)由(1)知,AM⊥面D′EF,所以平面ABCM⊥面D′EF,过D′作D′H⊥EF,则D′H⊥平面ABCM,,∠D′FH是直线D'F与平面ABCM所成角,∠D′AH是直线AD′与平面ABCM所成角在直角三角形D′AH求解即可.
【考点精析】根据题目的已知条件,利用直线与平面垂直的性质和空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握垂直于同一个平面的两条直线平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则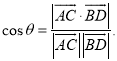 .
.