Question

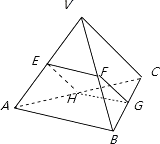
【题目】正三棱锥V﹣ABC的底面边长为2，E，F，G，H分别是VA，VB，BC，AC的中点，则四边形EFGH的面积的取值范围是

Answer 1

【答案】（ ，+∞）
【解析】解：由条件可知：EF=HG=1，EFGH是平行四边形，
因为正三棱锥V﹣ABC，所以EFGH是矩形而EH，FG，是变量，
当V点在ABC平面时，VA=VB=VC= ，
此时EH，FG有最小值，EH=FG= VA= ，
EFGH的面积为：EFEH=1× = ．
∴四边形EFGH的面积的取值范围是（ ，+∞）．
所以答案是：（ ，+∞）．

【考点精析】解答此题的关键在于理解棱锥的结构特征的相关知识，掌握侧面、对角面都是三角形；平行于底面的截面与底面相似，其相似比等于顶点到截面距离与高的比的平方．