题目内容
【题目】某物流公司购买了一块长AM＝30米，宽AN＝20米的矩形地块，计划把图中矩形ABCD建设为仓库，其余地方为道路和停车场，要求顶点C在地块对角线MN上，B、D分别在边AM、AN上，假设AB的长度为x米
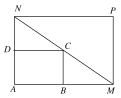
(1)求矩形ABCD的面积S关于x的函数解析式；
(2)要使仓库占地ABCD的面积不少于144平方米，则AB的长度应在什么范围内？
【答案】(1) S＝20x－
x2(0<x<30)(2)[12,18]．
【解析】
(1) 根据三角形相似，利用x表示出AD，进而用x表示出矩形ABCD的面积。
(2) 根据面积不小于144平方米，列出一元二次不等式，解不等式即可。
(1)根据题意，得△NDC与△NAM相似，所以
，即
，解得AD＝20－x.
所以矩形ABCD的面积S关于x的函数为S＝20x－x2(0<x<30)．
(2)要使仓库占地ABCD的面积不少于144平方米，即20x－x2≥144，化简得x2－30x＋216≤0，解得12≤x≤18，所以AB的长度的取值范围为[12,18]．
练习册系列答案
相关题目
【题目】某工厂生产甲、乙两种产品.已知生产一吨甲产品、一吨乙产品所需要的煤、电以及产值如表所示；又知道国家每天分配给该厂的煤和电力有限制，每天供煤至多56吨，供电至多45千瓦.问该厂如何安排生产，才能使该厂日产值最大？最大的产值是多少？
用煤（吨） | 用电（千瓦） | 产值（万元） | |
生产一吨 甲种产品 | 7 | 2 | 8 |
生产一吨 乙种产品 | 3 | 5 | 11 |
