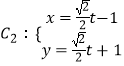题目内容
【题目】已知△ABC的三边所在直线的方程分别是lAB:4x-3y+10=0,lBC:y=2,lCA:3x-4y=5.
(1)求∠BAC的平分线所在直线的方程;
(2)求AB边上的高所在直线的方程.
【答案】(1)7x-7y+5=0;(2)3x+4y-21=0.
【解析】
(1)设P(x,y)是∠BAC的平分线上任意一点,根据点P到AC,AB的距离相等求出∠BAC的平分线所在直线的方程.(2) 设过点C的直线系方程为3x-4y-5+λ(y-2)=0,根据此直线与直线lAB:4x-3y+10=0垂直得到λ的值,即得AB边上的高所在直线的方程.
(1)设P(x,y)是∠BAC的平分线上任意一点,
则点P到AC,AB的距离相等,即![]() =
=![]() ,
,
∴4x-3y+10=±(3x-4y-5).
又∵∠BAC的平分线所在直线的斜率在![]() 和
和![]() 之间,
之间,
∴7x-7y+5=0为∠BAC的平分线所在直线的方程.
(2)设过点C的直线系方程为3x-4y-5+λ(y-2)=0,
即3x-(4-λ)y-5-2λ=0.
若此直线与直线lAB:4x-3y+10=0垂直,
则3×4+3(4-λ)=0,解得λ=8.
故AB边上的高所在直线的方程为3x+4y-21=0.

练习册系列答案
相关题目