题目内容
【题目】设数列{an}的前n项和为Sn . 若对n∈N* , 总k∈N* , 使得Sn=ak , 则称数列{an}是“G数列”. (Ⅰ)若数列{an}是等差数列,其首项a1=1,公差d=﹣1.证明:数列{an}是“G数列”;
(Ⅱ)若数列{an}的前n项和Sn=3n(n∈N*),判断数列{an}是否为“G数列”,并说明理由;
(Ⅲ)证明:对任意的等差数列{an},总存在两个“G数列”{bn}和{cn},使得an=bn+cn(n∈N*)成立.
【答案】解:(1)证明:由题意an=1+(n﹣1)(﹣1)=2﹣n, ![]() ,
,
若 ![]() ,
,
则 ![]() .
.
所以,存在k∈N* , 使得Sn=ak .
所以,数列{an}是“G数列.
(Ⅱ)首先a1=S1=3,
当n≥2时, ![]() ,
,
所以 ![]()
当n=2时,9=2×3k﹣1 , 得kN*因此数列{an}不是“G数列”.
(Ⅲ)若dn=bn,(b为常数),
则数列{dn}的前n项和 ![]() 是数列{dn}中的第
是数列{dn}中的第 ![]() 项,因此数列{dn}是“G数列”.
项,因此数列{dn}是“G数列”.
对任意的等差数列{an},an=a1+(n﹣1)d,(d为公差),
设bn=na1 , cn=(d﹣a1)(n﹣1),
则an=bn+cn , 而数列{bn}和{cn}都是“G数列”.
【解析】(Ⅰ)根据G数列的定义证明即可,(Ⅱ)由 ![]() ,可以判断数列{an}不是“G数列”,(Ⅲ)若dn=bn,(b为常数),可与判断数列{dn}是“G数列”,继而可以证明an=bn+cn(n∈N*)成立.
,可以判断数列{an}不是“G数列”,(Ⅲ)若dn=bn,(b为常数),可与判断数列{dn}是“G数列”,继而可以证明an=bn+cn(n∈N*)成立.
【考点精析】利用数列的前n项和和数列的通项公式对题目进行判断即可得到答案,需要熟知数列{an}的前n项和sn与通项an的关系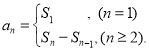 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.

练习册系列答案
相关题目