Question

【题目】如图，PD垂直正方形ABCD所在平面，AB＝2，E是PB的中点， ， >．

（1）建立适当的空间坐标系，求出点E的坐标；

（2）在平面PAD内求一点F，使EF⊥平面PCB．

Answer 1

【答案】（1）点E坐标是（1，1，1）（2）点F的坐标是（1，0，0）

【解析】试题分析：

(1)由题意，分别以DA、DC、DP所在直线分别为x轴、y轴、z轴建立空间坐标系，结合空间中点的坐标，设P（0，0，2m），则（1，1，m），结合平面向量夹角公式得到关于m的方程，解方程可得点E坐标是（1，1，1）；

(2)由题意，设F（x，0，z），结合平面向量的法向量和直线的方向向量得到关于坐标的方程组，求解方程组可得即点F是AD的中点．

试题解析：

（1）分别以DA、DC、DP所在直线分别为x轴、y轴、z轴建立空间坐标系，如图，则

（2，0，0），B（2，2，0），C（0，2，0），

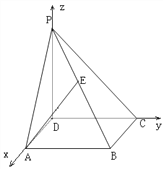
设P（0，0，2m），则（1，1，m），

∴　（-1，1，m），＝（0，0，2m）

∴　， ．

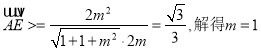∴　点E坐标是（1，1，1）；

（2）∵平面PAD，　∴　可设F（x，0，z）

＝（x-1，-1，z-1）， 又EF⊥平面PCB，　

∴　 ，-1， 2，0， =0，解得, ；

又∵　∴　，-1， 0，2，-2

∴　点F的坐标是（1，0，0），即点F是AD的中点．