题目内容
已知公比不为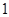 的等比数列
的等比数列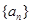 的首项
的首项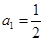 ,前
,前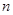 项和为
项和为 ,且
,且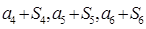 成等差数列.
成等差数列.
(1)求等比数列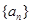 的通项公式;
的通项公式;
(2)对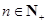 ,在
,在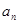 与
与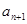 之间插入
之间插入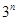 个数,使这
个数,使这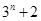 个数成等差数列,记插入的这
个数成等差数列,记插入的这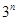 个数的和为
个数的和为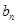 ,求数列
,求数列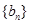 的前
的前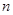 项和
项和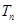 .
.
(1) 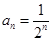 ;(2)
;(2) 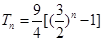
解析试题分析:(1)因为已知公比不为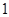 的等比数列
的等比数列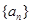 的首项
的首项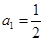 ,前
,前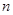 项和为
项和为 ,且
,且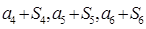 成等差数列.由等比数列的通项公式可求得数列
成等差数列.由等比数列的通项公式可求得数列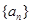 的通项公式.
的通项公式.
(2)由在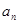 与
与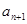 之间插入
之间插入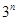 个数,使这
个数,使这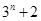 个数成等差数列,由等差数列的前n项和公式可求得,这
个数成等差数列,由等差数列的前n项和公式可求得,这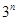 项的和为插入的这
项的和为插入的这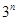 个数的和为
个数的和为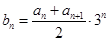 ,由(1)可求得
,由(1)可求得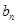 的表达式,再根据等比数列的前n项和公式即可得到结论.
的表达式,再根据等比数列的前n项和公式即可得到结论.
试题解析:(1)因为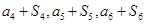 成等差数列,
成等差数列,
所以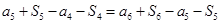 , 2分
, 2分
即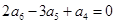 ,所以
,所以 ,因为
,因为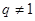 ,所以
,所以 , 4分
, 4分
所以等比数列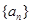 的通项公式为
的通项公式为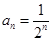 ; 6分
; 6分
(2) , 9分
, 9分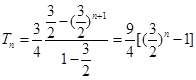 . 12分
. 12分
考点:1.等差等比数列.2.数列的前n项和公式.3.递推归纳的数学思想.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
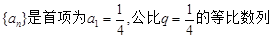 ,设数列
,设数列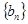 满足
满足 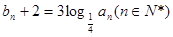 .
.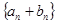 的前
的前 项和为
项和为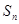 ;
; ,若
,若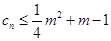 对一切正整数
对一切正整数 的取值范围.
的取值范围.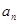 }、{
}、{  }满足:
}满足: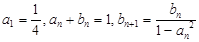 .
.
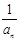 }为等差数列,并求数列
}为等差数列,并求数列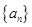 和{
和{  ,求实数
,求实数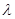 为何值时
为何值时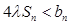 恒成立.
恒成立.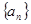 是等差数列,且
是等差数列,且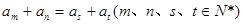 ,
,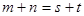 ;
;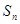 是等差数列
是等差数列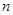 项的和,则
项的和,则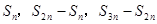 成等差数列;
成等差数列;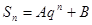 ;(其中
;(其中 是非零常数,
是非零常数,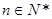 ),则
),则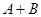 为零.
为零. 是首项为a,公差为d的等差数列
是首项为a,公差为d的等差数列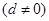 ,
, 是其前n项的和。记
是其前n项的和。记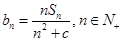 ,其中c为实数。
,其中c为实数。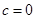 ,且
,且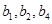 成等比数列,证明:
成等比数列,证明: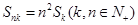 ;
;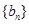 是等差数列,证明:
是等差数列,证明: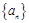 中,
中,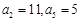 .
.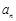 ;
; 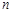 项和
项和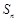 的最大值.
的最大值.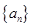 的首项
的首项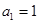 ,公差
,公差 ,且
,且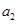 、
、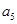 、
、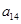 分别是等比数列
分别是等比数列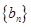 的
的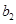 、
、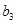 、
、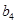 .
.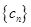 对任意正整数
对任意正整数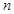 均有
均有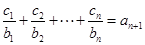 成立,求
成立,求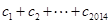 的值.
的值.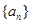 是公差不为0的等差数列,
是公差不为0的等差数列,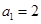 ,且
,且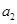 ,
,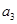 ,
,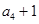 成等比数列.
成等比数列.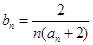 ,求数列
,求数列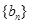 的前
的前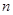 项和
项和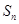 。
。