题目内容
设 是首项为a,公差为d的等差数列
是首项为a,公差为d的等差数列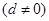 ,
, 是其前n项的和。记
是其前n项的和。记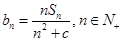 ,其中c为实数。
,其中c为实数。
(1)若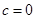 ,且
,且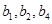 成等比数列,证明:
成等比数列,证明: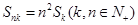 ;
;
(2)若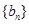 是等差数列,证明:
是等差数列,证明: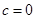 。
。
(1)见解析(2)见解析
解析试题分析:
(1)根据题意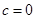 时,可得
时,可得 ,即得到
,即得到 通项,则可根据
通项,则可根据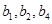 成等比数列,得到
成等比数列,得到 关系,从而将
关系,从而将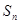 化为关于
化为关于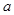 的式子.进而证明结论.
的式子.进而证明结论.
(2) 根据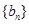 是等差数列,可设出
是等差数列,可设出 ,则有
,则有 ,将
,将 代入,化简该式为
代入,化简该式为 样式,通过令
样式,通过令 ,建立方程组,可解得
,建立方程组,可解得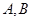 .则可讨论出
.则可讨论出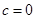 .
.
试题解析:
由题意可知 .①
.①
(1)由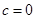 ,得
,得 .
.
又因为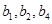 成等比数列,所以
成等比数列,所以 ,
,
即 ,化简得
,化简得 .
.
因为 ,所以
,所以 .因此对于所有的
.因此对于所有的 ,①有
,①有 .
.
从而对于所有的 ,有
,有 。
。
(2)设数列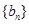 的公差为
的公差为 ,则
,则 ,
,
即 ,代入
,代入 的表达式,整理得,对于所有的
的表达式,整理得,对于所有的 ,
,
有 .
.
令 ,
,
则对于所有的 ,有
,有 .(*)
.(*)
在(*)式中分别取 ,得
,得 ,
,
从而有 ①,
①, ②,
②, ③,
③,
由②③得 ,代入方程①,得
,代入方程①,得 ,从而
,从而 .
.
即 ,
, 。
。
若 ,则由
,则由 ,得
,得 ,与题设矛盾,所以
,与题设矛盾,所以 。
。
又因为 ,所以
,所以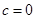 。
。
考点:等差数列前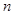 项和,等比中项;化繁为简的思想,等价代换的思想.
项和,等比中项;化繁为简的思想,等价代换的思想.

练习册系列答案
相关题目
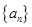 为正项等比数列,
为正项等比数列,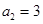 ,
,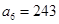 ,
,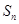 为等差数列
为等差数列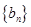 的前
的前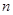
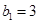 ,
,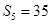 .
.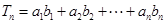 ,求
,求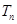 .
.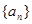 满足
满足 (
( ).
). ,
, (
( 和
和 的值,使得数列
的值,使得数列 为等比数列;并求此时数列
为等比数列;并求此时数列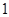 的等比数列
的等比数列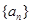 的首项
的首项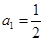 ,前
,前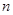 项和为
项和为 ,且
,且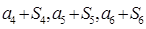 成等差数列.
成等差数列.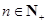 ,在
,在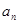 与
与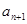 之间插入
之间插入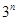 个数,使这
个数,使这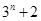 个数成等差数列,记插入的这
个数成等差数列,记插入的这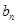 ,求数列
,求数列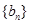 的前
的前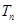 .
. 的前n项和为Sn,且满足
的前n项和为Sn,且满足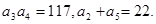
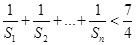 .
.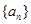 是公差不为零的等差数列,
是公差不为零的等差数列, ,且
,且 是
是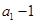 和
和 的等比中项,求:
的等比中项,求: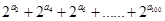 .
.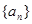 的公差不为零,其前n项和为
的公差不为零,其前n项和为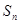 ,若
,若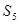 =70,且
=70,且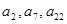 成等比数列,
成等比数列,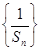 的前n项和为
的前n项和为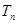 ,求证:
,求证: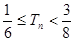 .
.