题目内容
已知数列{ 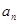 }、{
}、{  }满足:
}满足: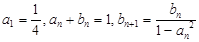 .
.
(1)求
(2)证明:数列{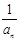 }为等差数列,并求数列
}为等差数列,并求数列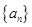 和{
和{  }的通项公式;
}的通项公式;
(3)设 ,求实数
,求实数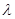 为何值时
为何值时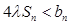 恒成立.
恒成立.
(1)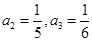 ;(2)证明见解析,
;(2)证明见解析,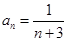 ,
,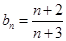 ;(3)
;(3)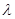 ≤1.
≤1.
解析试题分析:(1)递推依次求得;(2)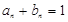 可得
可得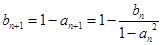 ,化简可证
,化简可证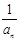 为等差数列,求出通项公式,进而求出
为等差数列,求出通项公式,进而求出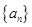 和{
和{  }的通项公式;(3)裂项法可求
}的通项公式;(3)裂项法可求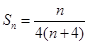 ,则代入
,则代入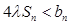 ,将原不等式恒成立转化为
,将原不等式恒成立转化为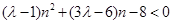 ,利用一元二次函数知识可得
,利用一元二次函数知识可得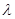 ≤1.
≤1.
解:(1) ∵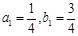 ,∴
,∴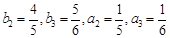 ; 4分
; 4分
(2)∵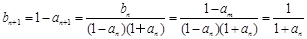 ,
,
∴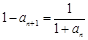 ,
,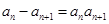 ,
,
∴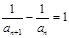 , ∴ 数列{
, ∴ 数列{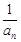 }是以4为首项,1为公差的等差数列, 6分
}是以4为首项,1为公差的等差数列, 6分
∴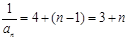 ,
, 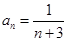 , ∴
, ∴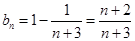 ; 8分
; 8分
(3) 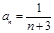 , ∴
, ∴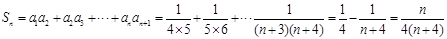 ,
,
∴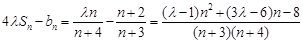 , 10分
, 10分
由条件可知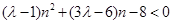 恒成立即可满足条件,
恒成立即可满足条件,
设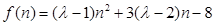 ,
,
当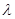 =1时,
=1时,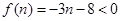 恒成立,
恒成立,
当 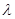 >1时,由二次函数的性质知不可能成立,
>1时,由二次函数的性质知不可能成立,
当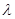 <l时,对称轴
<l时,对称轴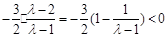 , 13分
, 13分
f(n)在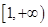 为单调递减函数,
为单调递减函数,  ,
,
∴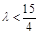 ∴
∴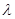 <1时
<1时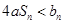 恒成立,
恒成立,
综上知: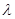 ≤1时,
≤1时,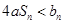 恒成立. 14分
恒成立. 14分
考点:等差数列的定义,裂项法求和,不等式恒成立.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
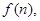 试写出
试写出 的表达式;
的表达式;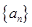 的首项
的首项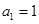 ,公差
,公差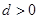 ,数列
,数列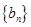 是等比数列,且
是等比数列,且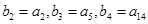 .
.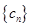 对任意正整数n,均有
对任意正整数n,均有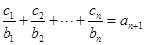 成立,求
成立,求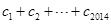 的值.
的值.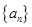 为正项等比数列,
为正项等比数列,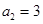 ,
,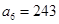 ,
,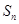 为等差数列
为等差数列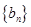 的前
的前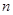
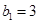 ,
,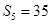 .
.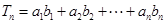 ,求
,求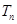 .
.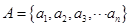 ,
,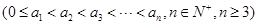
 :对任意的
:对任意的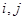
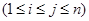 ,
,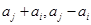 至少有一个属于
至少有一个属于 .
.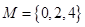 与
与 是否具有性质
是否具有性质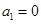 ;
;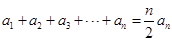 ;
;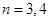 或
或 时集合
时集合 是否一定成等差数列?说明理由.
是否一定成等差数列?说明理由.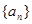 满足
满足 (
( ).
). ,
, (
( 和
和 的值,使得数列
的值,使得数列 为等比数列;并求此时数列
为等比数列;并求此时数列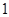 的等比数列
的等比数列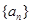 的首项
的首项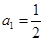 ,前
,前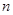 项和为
项和为 ,且
,且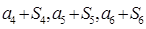 成等差数列.
成等差数列.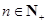 ,在
,在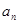 与
与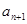 之间插入
之间插入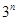 个数,使这
个数,使这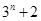 个数成等差数列,记插入的这
个数成等差数列,记插入的这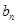 ,求数列
,求数列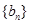 的前
的前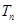 .
.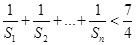 .
.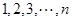 中这
中这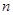 个数中取
个数中取 (
( ,
,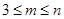 )个数组成递增等差数列,所有可能的递增等差数列的个数记为
)个数组成递增等差数列,所有可能的递增等差数列的个数记为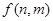 .
.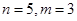 时,写出所有可能的递增等差数列及
时,写出所有可能的递增等差数列及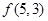 的值;
的值;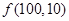 ;
;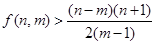 .
.