题目内容
已知在等差数列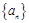 中,
中,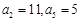 .
.
(1)求通项公式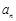 ;
;
(2)求前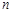 项和
项和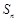 的最大值.
的最大值.
(1) ,(2)
,(2)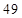 .
.
解析试题分析:(1)求等差数列通项,通常用待定系数法,即设 的公差为
的公差为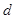 及首项,列出两个独立条件:
及首项,列出两个独立条件: ,解得
,解得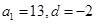 ,再代入通项公式即可:
,再代入通项公式即可: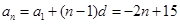 ,(2)求等差数列前
,(2)求等差数列前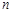 项和
项和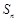 的最大值,一般用两个方法,一是函数思想,即利用等差数列前
的最大值,一般用两个方法,一是函数思想,即利用等差数列前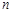 项和公式,将
项和公式,将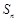 表示为关于
表示为关于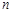 的二次函数,利用二次函数定义区间与对称轴的位置关系求最值,此法注意去最值时自变量须是正整数这一限制条件,二是利用等差数列项的单调性,求出所有正项的和即为前
的二次函数,利用二次函数定义区间与对称轴的位置关系求最值,此法注意去最值时自变量须是正整数这一限制条件,二是利用等差数列项的单调性,求出所有正项的和即为前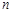 项和
项和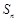 的最大值.
的最大值.
试题解析:(1)设 的公差为
的公差为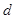 ,由已知条件,得
,由已知条件,得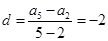 ,
,
解得 , 2分
, 2分
所以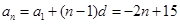 .(
.(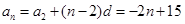 )5分
)5分
或 ,得
,得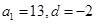 ,所以
,所以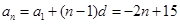
(2)
 .8分
.8分
所以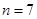 时,
时,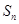 取到最大值
取到最大值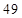 .10分
.10分
考点:等差数列前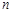 项和最值
项和最值

练习册系列答案
相关题目
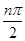 -bn·cos2
-bn·cos2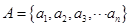 ,
,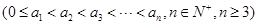
 :对任意的
:对任意的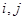
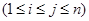 ,
,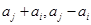 至少有一个属于
至少有一个属于 .
.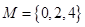 与
与 是否具有性质
是否具有性质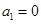 ;
;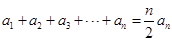 ;
;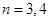 或
或 时集合
时集合 是否一定成等差数列?说明理由.
是否一定成等差数列?说明理由.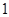 的等比数列
的等比数列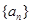 的首项
的首项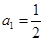 ,前
,前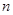 项和为
项和为 ,且
,且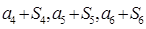 成等差数列.
成等差数列.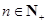 ,在
,在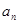 与
与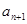 之间插入
之间插入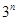 个数,使这
个数,使这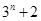 个数成等差数列,记插入的这
个数成等差数列,记插入的这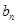 ,求数列
,求数列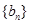 的前
的前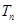 .
.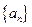 的前
的前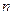 项和为
项和为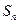 .已知
.已知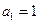 ,
,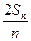 =an+1-
=an+1-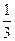 n2-n-
n2-n-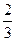 (
(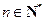 )
)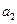 的值;
的值;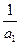 +
+ +…+
+…+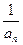 <
<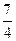 .
.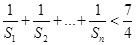 .
.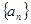 满足
满足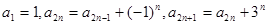 (
( ).
). 的值;
的值;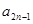 (用含
(用含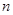 的式子表示);
的式子表示); ,数列
,数列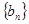
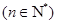 的前
的前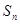 ,求
,求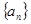 是等差数列,且
是等差数列,且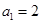 且
且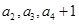 成等比数列。
成等比数列。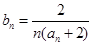 ,求前n项和
,求前n项和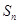 .
.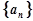 的前n项和为
的前n项和为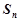 ,
,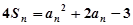 ,且
,且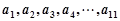 成等比数列,当
成等比数列,当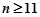 时,
时,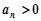 .
.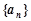 成等差数列;
成等差数列;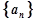 的前n项和
的前n项和