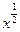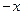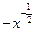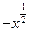题目内容
(本小题满分14分) 已知函数f (x)＝ex－k－x，其中x∈R． (1)当k＝0时，若g(x)＝
定义域为R，求实数m的取值范围；(2)给出定理：若函数f (x)在[a，b]上连续，且f (a)·f (b)<0，则函数y＝f (x)在区间(a，b)内有零点，即存在x0∈(a，b)，使f (x0)＝0；运用此定理，试判断当k>1时，函数f (x)在(k，2k)内是否存在零点．
定义域为R，求实数m的取值范围；(2)给出定理：若函数f (x)在[a，b]上连续，且f (a)·f (b)<0，则函数y＝f (x)在区间(a，b)内有零点，即存在x0∈(a，b)，使f (x0)＝0；运用此定理，试判断当k>1时，函数f (x)在(k，2k)内是否存在零点．(Ⅰ)
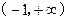
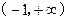
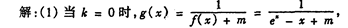
练习册系列答案
相关题目
P>0时，若对任意x>0，恒有f(x)≤0,求P的取值范围（2）证明：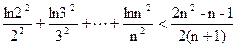
(n∈N
，n≥2)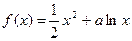
（a∈R）．(1)若
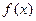在[1，e]上是增函数，求a的取值范围（2）若a=1,a≤x≤e,证明：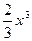
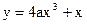, 过点Q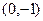
作C的切线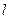
, 切点为P.
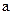怎样变化, 点P总在一条定直线上;
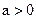, 过点P且与
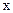轴交于点T, 求
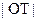的最小值(O为原点).
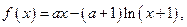其中
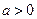。（1）求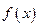
的单调区间；
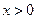时，证明不等式：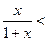
；
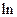
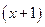
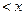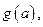证明不等式：
。
(
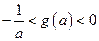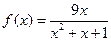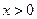) , (Ⅰ)试确定
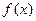的单调区间 , 并证明你的结论 ;(Ⅱ)若
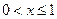时 , 不等式
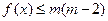恒成立 , 求实数
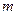的取值范围 . 
的导函数
，则数列
的前n项和是
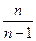
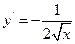，则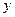
的表达式为（ ）
