题目内容
【题目】在平面直角坐标系![]() 中,椭圆E:
中,椭圆E:![]() (
(![]() )的长轴长为4,左准线l的方程为
)的长轴长为4,左准线l的方程为![]() .
.
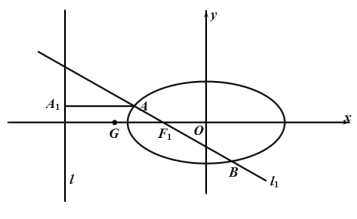
(1)求椭圆的标准方程;
(2)直线![]() 过椭圆E的左焦点
过椭圆E的左焦点![]() ,且与椭圆E交于A,B两点.
,且与椭圆E交于A,B两点.
①若![]() ,求直线
,求直线![]() 的方程;
的方程;
②过A作左准线l的垂线,垂足为![]() ,点
,点![]() ,求证:
,求证:![]() ,B,G三点共线.
,B,G三点共线.
【答案】(1)![]() (2)①
(2)①![]() 或
或![]() ,②证明见解析
,②证明见解析
【解析】
(1)根据长轴的值和准线的方程,可求得![]() ,
,![]() 的值,结合
的值,结合![]() ,从而可求出椭圆的标准方程;
,从而可求出椭圆的标准方程;
(2)①设![]() ,
,![]() ,作
,作![]() ,根据椭圆的第二定义可得
,根据椭圆的第二定义可得![]() ,结合
,结合![]() ,可推出
,可推出![]() ,从而推出
,从而推出![]() ,根据
,根据![]() ,可得
,可得![]() ,分别对直线
,分别对直线![]() 的斜率存在与不存在进行讨论,结合韦达定理即可求得直线
的斜率存在与不存在进行讨论,结合韦达定理即可求得直线![]() 的方程;
的方程;
②当直线![]() 的斜率不存在时,分别求出
的斜率不存在时,分别求出![]() ,
,![]() ,即可得证;当直线
,即可得证;当直线![]() 的斜率存在时,分别求出
的斜率存在时,分别求出![]() ,
,![]() ,结合韦达定理即可求证.
,结合韦达定理即可求证.
(1)由题,![]() ,
,![]() ,∴
,∴![]() ,
,![]()
∴![]() ,椭圆方程
,椭圆方程![]() .
.
(2)①设![]() ,
,![]()
作![]() ,由第二定义,
,由第二定义,![]() ,而
,而![]()
∴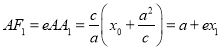 ,同理
,同理![]()
∴![]() ,即
,即![]() ,②证明见解析
,②证明见解析
设![]() 的斜率为k
的斜率为k
1°若k不存在,即![]() (舍)
(舍)
2°若k存在,![]() :
:![]()
联立
消去y,![]() (*),
(*),![]() 恒成立
恒成立
∴![]() ,即
,即![]() ,∴
,∴![]() :
:![]() 或
或![]()
②证明1°若![]() 的斜率不存在,
的斜率不存在,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
∴![]() ,B,G三点共线.
,B,G三点共线.
2°若![]() 的斜率存在,
的斜率存在,![]() ,
,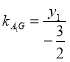 ,
,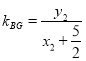
要证![]() ,B,G共线.即证
,B,G共线.即证![]() ,即
,即![]() ,即
,即![]()
即![]() ,即
,即![]()
由(*)![]() ,
,![]()
代入上式:![]() ,即
,即![]() 显然成立。
显然成立。
∴![]() ,B,G三点共线.
,B,G三点共线.
综上所述,![]() ,B,G三点共线.
,B,G三点共线.

练习册系列答案
相关题目