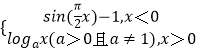题目内容
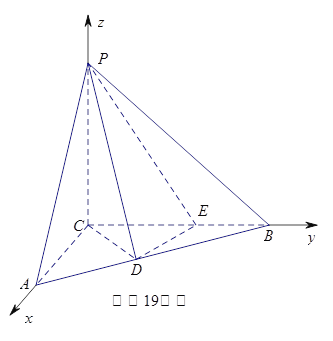
【题目】如图,三棱锥![]() 中,
中,![]() 平面
平面

![]() ,
,![]() ,
,![]() 。
。![]() 分别为线段
分别为线段![]() 上的点,且
上的点,且![]() 。
。
(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值。
的余弦值。
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)要证线面垂直,就是要证线线垂直,题中由![]() 平面
平面![]() ,可知
,可知![]() ,再分析已知由
,再分析已知由![]() 得
得![]() ,这样与
,这样与![]() 垂直的两条直线都已找到,从而可得线面垂直;(2)求二面角的大小,可心根据定义作出二面角的平面角,求出这个平面角的大小,本题中,由于
垂直的两条直线都已找到,从而可得线面垂直;(2)求二面角的大小,可心根据定义作出二面角的平面角,求出这个平面角的大小,本题中,由于![]() ,
,![]() 平面
平面![]() ,因此
,因此![]() 两两垂直,可以他们为
两两垂直,可以他们为![]() 轴建立空间直角坐标系,写出图中各点的坐标,求出平面
轴建立空间直角坐标系,写出图中各点的坐标,求出平面![]() 和平面
和平面![]() 的法向量
的法向量![]() ,向量
,向量![]() 的夹角与二面角相等或互补,由此可得结论.
的夹角与二面角相等或互补,由此可得结论.
试题解析:(1)证明:由PC![]() 平面ABC,DE
平面ABC,DE![]() 平面ABC,故PC
平面ABC,故PC![]() DE
DE
由CE=2,CD=DE=![]() 得
得![]() CDE为等腰直角三角形,故CD
CDE为等腰直角三角形,故CD![]() DE
DE
由PC![]() CD=C,DE垂直于平面PCD内两条相交直线,故DE
CD=C,DE垂直于平面PCD内两条相交直线,故DE![]() 平面PCD
平面PCD
(2)解:由(1)知,![]() CDE为等腰直角三角形,
CDE为等腰直角三角形,![]() DCE=
DCE=![]() ,如(19)图,过点D作DF垂直CE于F,易知DF=FC=EF=1,又已知EB=1,
,如(19)图,过点D作DF垂直CE于F,易知DF=FC=EF=1,又已知EB=1,
故FB=2.
由![]() ACB=
ACB=![]() 得DF
得DF![]() AC,
AC,![]() ,故AC=
,故AC=![]() DF=
DF=![]() .
.
以C为坐标原点,分别以![]() 的方程为x轴,y轴,z轴的正方向建立空间直角坐标系,则C(0,0,0,),P(0,0,3),A(
的方程为x轴,y轴,z轴的正方向建立空间直角坐标系,则C(0,0,0,),P(0,0,3),A(![]() ,0,0),E(0,2,0),D(1,1,0),
,0,0),E(0,2,0),D(1,1,0),![]()
![]()
设平面![]() 的法向量
的法向量![]() ,
,
由![]() ,
,![]() ,
,
得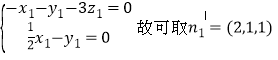 .
.
由(1)可知DE![]() 平面PCD,故平面PCD的法向量
平面PCD,故平面PCD的法向量![]() 可取为
可取为![]() ,即
,即![]() .
.
从而法向量![]() ,
,![]() 的夹角的余弦值为
的夹角的余弦值为 ,
,
故所求二面角A-PD-C的余弦值为![]() .
.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目