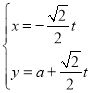题目内容
【题目】已知![]() 中,内角
中,内角![]() 、
、![]() 、
、![]() 的对边为
的对边为![]() 、
、![]() 、
、![]() ,
,![]() 三角形
三角形![]() 外接圆的半径,证明:
外接圆的半径,证明:
(1)![]() ;
;
(2)![]() .
.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)采用坐标法证明,方法是以![]() 为原点,
为原点,![]() 所在的直线为
所在的直线为![]() 轴建立平面直角坐标系,表示出点
轴建立平面直角坐标系,表示出点![]() 和点
和点![]() 的坐标,利用两点间的距离公式表示出
的坐标,利用两点间的距离公式表示出![]() ,化简后即得到
,化简后即得到![]() ;
;
(2)作出三角形的外接圆,分角![]() 为锐角、直角、钝角三种情况讨论,构造直角三角形,利用同弧所对的圆周角相等结合锐角三角函数的定义以及诱导公式证明出
为锐角、直角、钝角三种情况讨论,构造直角三角形,利用同弧所对的圆周角相等结合锐角三角函数的定义以及诱导公式证明出![]() ,同理可证明出
,同理可证明出![]() ,进而得出结论.
,进而得出结论.
(1)已知![]() 中,内角
中,内角![]() 、
、![]() 、
、![]() 的对边为
的对边为![]() 、
、![]() 、
、![]() ,
,
以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴建立直角坐标系,
轴建立直角坐标系,
则![]() ,
,![]() ,
,
则![]()
![]() ,故得证;
,故得证;
(2)在![]() 中,设
中,设![]() ,
,![]() ,
,![]() .
.
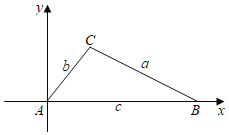
若![]() 为锐角,如下图所示,过点
为锐角,如下图所示,过点![]() 作
作![]() 的垂线交
的垂线交![]() 的外接圆于点
的外接圆于点![]() ,连接
,连接![]() ,则
,则![]() ,
,
由同弧所对的圆周角相等可得![]() ,
,
由锐角三角函数的定义可得,![]() ,
,![]() ;
;
若![]() 为直角,则
为直角,则![]() ,
,![]() ,此时
,此时![]() 成立;
成立;
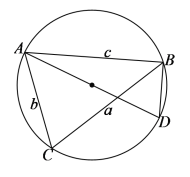
若![]() 为钝角,如下图所示:
为钝角,如下图所示:
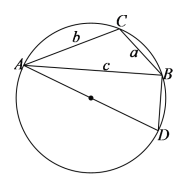
过点![]() 作
作![]() 的垂线交
的垂线交![]() 的外接圆于点
的外接圆于点![]() ,连接
,连接![]() ,则
,则![]() ,且
,且![]() ,
,
由锐角三角函数的定义可得,![]() ,
,
![]() .
.
同理可证明出![]() ,因此,
,因此,![]() .
.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案【题目】为了增强消防意识,某部门从男,女职工中各随机抽取了20人参加消防知识测试(满分为100分),这40名职工测试成绩的茎叶图如下图所示

(1)根据茎叶图判断男职工和女职工中,哪类职工的测试成绩更好?并说明理由;
(2)(ⅰ)求这40名职工成绩的中位数![]() ,并填写下面列联表:
,并填写下面列联表:
超过 | 不超过 | |
男职工 | ||
女职工 |
(ⅱ)如果规定职工成绩不少于m定为优秀,根据(ⅰ)中的列联表,能否有99%的把握认为消防知识是否优秀与性别有关?
附: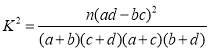 .
.
P( | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
【题目】某品牌汽车4S店,对该品牌旗下的A型、B型、C型汽车进行维修保养,汽车4S店记录了100辆该品牌三种类型汽车的维修情况,整理得下表:
车型 | A型 | B型 | C型 |
频数 | 20 | 40 | 40 |
假设该店采用分层抽样的方法从上述维修的100辆该品牌三种类型汽车中随机取10辆进行问卷回访.
(1)求A型、B型、C型各车型汽车抽取的数目;
(2)维修结束后这100辆汽车的司机采用“100分制”打分的方式表示对4S店的满意度,按照大于等于80为优秀,小于80为合格,得到如下列联表:
优秀 | 合格 | 合计 | |
男司机 | 10 | 38 | 48 |
女司机 | 25 | 27 | 52 |
合计 | 35 | 65 | 100 |
问能否在犯错误概率不超过0.01的前提下认为司机对4S店满意度与性别有关系?请说明原因.
(参考公式: )
)
附表:
| 0.100 | 0.050 | 0.010 | 0.001 |
K | 2.706 | 3.841 | 6.635 | 10.828 |