Question

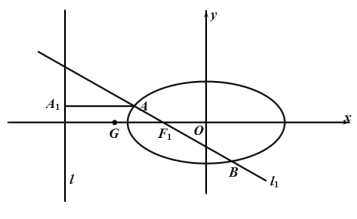
【题目】如图①，是由矩形，和组成的一个平面图形，其中，，将其沿折起使得重合，连接如图②.

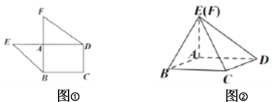
（1）证明：平面平面；

（2）若为线段中点，求直线与平面所成角的正切值.

Answer 1

【答案】（1）证明见解析（2）

【解析】

（1）由翻折变换的性质，先证明平面，平面，又平面，所以平面平面．

（2）过作的垂线，连接，直线和平面所成的角为，中，，得出结论．

解：（1）证明：由翻折变换的性质：，，，

平面，平面，

平面，

平面，

所以，

又因为，，平面，平面．

所以平面．

又因为平面，所以平面平面．

（2）过作的垂线，垂足为，连接，有，平面，

所以平面，因为平面

所以，直线和平面所成的角为，

由为的中点，，所以为的中点，

所以，，又，在中，，

中，，

故直线与平面所成角的正切值为．