题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,判断函数
,判断函数![]() 的单调性并说明理由;
的单调性并说明理由;
(2)若![]() ,求证:关
,求证:关![]() 的不等式
的不等式![]() 在
在![]() 上恒成立.
上恒成立.
【答案】(1)函数![]() 在
在![]() 上单调递减,理由见解析;(2)证明见解析.
上单调递减,理由见解析;(2)证明见解析.
【解析】
(1)求出函数![]() 的导数,分析导数
的导数,分析导数![]() 在区间
在区间![]() 上的符号,即可得出结论;
上的符号,即可得出结论;
(2)将所证不等式变形为![]() ,证明出
,证明出![]() ,于是将不等式转化为证明
,于是将不等式转化为证明![]() ,通过证明出
,通过证明出![]() ,将不等式转化为
,将不等式转化为![]() ,然后构造函数
,然后构造函数![]() ,利用单调性证明即可.
,利用单调性证明即可.
(1)函数![]() 在
在![]() 上单调递减,理由如下:
上单调递减,理由如下:
依题意![]() ,
,![]() ,则
,则 .
.
当![]() 时,
时,![]() ,故函数
,故函数![]() 在
在![]() 上单调递减;
上单调递减;
(2)要证![]() ,即证
,即证![]() ,
,
即证![]() .
.
设![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() .
.
故当![]() 时,
时,![]() ,
,
故即证![]() .
.
令![]() ,
,![]() .
.
由(1)可知,![]() ,
,
故![]() 在
在![]() 上单调递增.
上单调递增.
所以,当![]() 时,
时,![]() ,即
,即![]() ,
,
所以,当![]() 时,
时,![]() ,
,
所以只需证明![]() ,即证明
,即证明![]() .
.
设![]() ,则
,则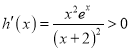 .
.
所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,所以原不等式成立.
,所以原不等式成立.

练习册系列答案
相关题目
【题目】为了增强消防意识,某部门从男,女职工中各随机抽取了20人参加消防知识测试(满分为100分),这40名职工测试成绩的茎叶图如下图所示

(1)根据茎叶图判断男职工和女职工中,哪类职工的测试成绩更好?并说明理由;
(2)(ⅰ)求这40名职工成绩的中位数![]() ,并填写下面列联表:
,并填写下面列联表:
超过 | 不超过 | |
男职工 | ||
女职工 |
(ⅱ)如果规定职工成绩不少于m定为优秀,根据(ⅰ)中的列联表,能否有99%的把握认为消防知识是否优秀与性别有关?
附: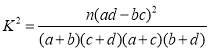 .
.
P( | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |