Question

【题目】如图，在四棱锥中，底面为正方形， 底面， ，过点的平面与棱， ， 分别交于点， ， （， ， 三点均不在棱的端点处）．　

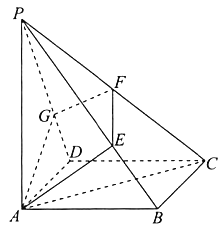
（Ⅰ）求证：平面平面；

（Ⅱ）若平面，求的值；

（Ⅲ）直线是否可能与平面平行？证明你的结论.

Answer 1

【答案】（Ⅰ）见解析;（Ⅱ）见解析;（Ⅲ）见解析.

【解析】试题分析：（Ⅰ）先用线面垂直的判定证明平面，可得平面平面．

（Ⅱ）由 且，得是的中点，所以 ．

（Ⅲ）反证法证明，假设平面，结合条件可得，平面平面，这显然矛盾！所以假设不成立，即与平面不可能平行．

试题解析：

：

（Ⅰ）因为平面，所以．因为为正方形，所以，所以平面．所以平面平面．

（Ⅱ）连接．因为 平面，所以 ．

又因为 ，所以 是的中点． 所以 ．

（Ⅲ）与平面不可能平行．

证明如下：假设平面，因为 ， 平面．所以 平面．而 平面，所以 平面平面，这显然矛盾！ 所以假设不成立，即与平面不可能平行．