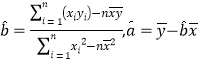题目内容
【题目】甲、乙两人做定点投篮游戏，已知甲每次投篮命中的概率均为
，乙每次投篮命中的概率均为
，甲投篮3次均未命中的概率为
，甲、乙每次投篮是否命中相互之间没有影响.
（1）若甲投篮3次，求至少命中2次的概率；
（2）若甲、乙各投篮2次，设两人命中的总次数为
，求
的分布列和数学期望.
【答案】（1）
（2）见解析
【解析】试题分析：（1）至少命中2次的事件包括恰好命中两次和恰好命中3次，再根据独立重复试验概率计算公式得概率，（2）先确定随机变量取法，再根据独立重复试验概率计算公式求对应概率，列表可得分布列，最后根据熟悉期望公式求期望
试题解析：解：（1）由题意， 
，解得
.
设“甲投篮3次，至少2次命中”为事件
，
则
.
（2）由题意
的取值为0，1，2，3，4.
；
；
；
.
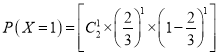
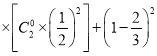
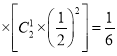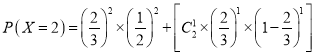
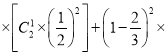
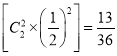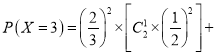
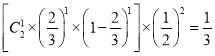
故
的分布列为
.
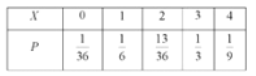
练习册系列答案
智慧课堂密卷100分单元过关检测系列答案
单元期中期末卷系列答案
相关题目
【题目】某厂需要确定加工某大型零件所花费的时间，连续4天做了4次统计，得到的数据如下：
零件的个数 | 2 | 3 | 4 | 5 |
加工的时间 | 2.5 | 3 | 4 | 5.5 |
（1）在直角坐标系中画出以上数据的散点图，求出
关于
的回归方程
，并在坐标系中画出回归直线；
（2）试预测加工10个零件需要多少时间？
参考公式：两个具有线性关系的变量的一组数据：
，
其回归方程为，其中
