Question

【题目】已知函数，设为曲线在点处的切线，其中.

（Ⅰ）求直线的方程（用表示）；

（Ⅱ）求直线在轴上的截距的取值范围；

（Ⅲ）设直线分别与曲线和射线（）交于， 两点，求的最小值及此时的值.

Answer 1

【答案】（Ⅰ）;（Ⅱ） ;（Ⅲ）， ．

【解析】试题分析：（Ⅰ） 对求导数，由此得切线的方程为： .

（Ⅱ）由（Ⅰ）得，直线在轴上的截距为．设新的函数， 求导，求最值即可.

（Ⅲ）过作轴的垂线，与射线交于点，得到△是等腰直角三角形， ．设 ， 求最值即可.

试题解析：

（Ⅰ） 对求导数，得， 所以切线的斜率为，由此得切线的方程为： ， 即 .

（Ⅱ） 由（Ⅰ）得，直线在轴上的截距为．

设 ， ．所以 ，令，得．

， 的变化情况如下表：

		↘		↘

所以函数在上单调递减，所以， ，

所以直线在轴上的截距的取值范围是．

（Ⅲ）过作轴的垂线，与射线交于点，

所以△是等腰直角三角形．所以 ．

设 ， ，

所以 ．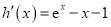

令 ，则，

所以 在上单调递增，

所以 ，

从而 在上单调递增，所以 ，此时， ．

所以 的最小值为，此时．

点晴:本题主要考查导数与切线，导数与最值问题. 解答此类问题，应该首先确定函数的定义域，第二问中利用导数把直线在轴上的截距为．设新的函数， 求导，求最值即可;第三问中借助几何关系．得到 ， 求最值即可.