题目内容
【题目】已知函数
是定义在
上的奇函数.
（1）求
的值和实数
的值；
（2）判断函数
在
上的单调性，并给出证明；
（3）若
且
求实数
的取值范围.
【答案】（1）
（2）增函数，见解析；（3）
【解析】试题分析：（1）直接把0代入即可求出f（0）的值；再结合f（﹣x）+f（x）=0对定义域内的所有自变量成立即可求出实数m的值；
（2）先研究内层函数的单调性，再结合复合函数的单调性即可判断函数f（x）在（﹣1，1）上的单调性；
（3）先根据
得到a的范围；再结合其为奇函数把f（b﹣2）+f（2b﹣2）＞0转化为f（b﹣2）＞f（2﹣2b），结合第二问的单调性即可求出实数b的取值范围．
试题解析：
（I）
因为
是奇函数。
所以： 
，
，
即
对定义域内的
都成立. 
.
所以
或
（舍）
.
（Ⅱ）
；
设
设
，则
.
当
时， 
在
上是增函数.
（Ⅲ）由
得
函数
是奇函数
，
，
由（Ⅱ）得
在
上是增函数
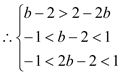
的取值范围是
练习册系列答案
相关题目
