题目内容
【题目】如图, ![]() 为等边三角形,
为等边三角形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.
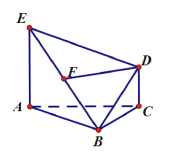
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() .
.
【答案】(1)见解析(2)见解析
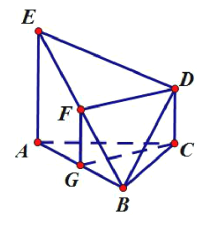
【解析】试题分析:(1)取AB的中点G,连结FG,GC,由三角形中位线定理可得FG∥AE, ![]() ,结合已知DC∥AE,
,结合已知DC∥AE, ![]() ,
, ![]() 可得四边形DCGF为平行四边形,得到FD∥GC,由线面平行的判定可得FD∥平面ABC;(2)由线面垂直的性质可得EA⊥面ABC,得到EA⊥GC,再由△ABC为等边三角形,得CG⊥AB,结合线面垂直的判定可得CG⊥平面EAB,再由面面垂直的判定可得面BDE⊥面EAB.
可得四边形DCGF为平行四边形,得到FD∥GC,由线面平行的判定可得FD∥平面ABC;(2)由线面垂直的性质可得EA⊥面ABC,得到EA⊥GC,再由△ABC为等边三角形,得CG⊥AB,结合线面垂直的判定可得CG⊥平面EAB,再由面面垂直的判定可得面BDE⊥面EAB.
解析:
(1)证明:取![]() 的中点
的中点![]() ,连结
,连结![]()
∵在![]() 中,
中, ![]() ,
, ![]()
∵![]() ,
, ![]() ∴
∴![]() ,
, ![]()
∴四边形![]() 为平行四边形 ∴
为平行四边形 ∴![]()
又∵![]() 平面
平面![]() ∴
∴![]() 平面
平面![]()
(2)证:∵![]() 面
面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() ,
,
又∵![]() 为等边三角形,∴
为等边三角形,∴![]() ,
,
又∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
又∵![]() ,∴
,∴![]() 面
面![]() ,
,
又∵![]() 面
面![]() ,∴面
,∴面![]() 面
面![]()

【题目】某公司为了研究年宣传费![]() (单位:千元)对销售量
(单位:千元)对销售量![]() (单位:吨)和年利润
(单位:吨)和年利润![]() (单位:千元)的影响,搜集了近 8 年的年宣传费
(单位:千元)的影响,搜集了近 8 年的年宣传费![]() 和年销售量
和年销售量![]() 数据:
数据:
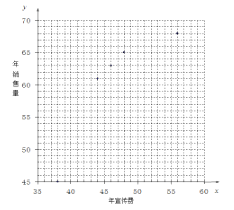
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 38 | 40 | 44 | 46 | 48 | 50 | 52 | 56 |
| 45 | 55 | 61 | 63 | 65 | 66 | 67 | 68 |
(Ⅰ)请补齐表格中 8 组数据的散点图,并判断![]() 与
与![]() 中哪一个更适宜作为年销售量
中哪一个更适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的函数表达式?(给出判断即可,不必说明理由)
的函数表达式?(给出判断即可,不必说明理由)
(Ⅱ)若(Ⅰ)中的![]() ,且产品的年利润
,且产品的年利润![]() 与
与![]() ,
, ![]() 的关系为
的关系为![]() ,为使年利润值最大,投入的年宣传费 x 应为何值?
,为使年利润值最大,投入的年宣传费 x 应为何值?
【题目】某同学参加学校自主招生3门课程的考试,假设该同学第一门课程取得优秀成绩概率为 ![]() ,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为
,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为
ξ | 0 | 1 | 2 | 3 |
p |
| x | y |
|
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率及求p,q的值;
(Ⅱ)求该生取得优秀成绩课程门数的数学期望Eξ.