已知关于x的方程x2-x+acosB=0的两根之积等于两根之和.且边a.b为△ABC的两内角A.B所对的边.则△ABC是( )A．等腰三角形B．等边三角形C．直角三角形D．等腰直角三角形题目和参考答案——青夏教育精英家教网—

题目内容

8．已知关于x的方程x²-（bcosA）x+acosB=0的两根之积等于两根之和，且边a，b为△ABC的两内角A，B所对的边，则△ABC是（　　）

A．

等腰三角形

B．

等边三角形

C．

直角三角形

D．

等腰直角三角形

分析由题意可得bcosA=acosB，由正弦定理可得sinBcosA=sinAcosB，由已知条件可判A=B，可得结论．

解答解：∵方程x²-（bcosA）x+acosB=0的两根之积等于两根之和，
∴bcosA=acosB，由正弦定理可得sinBcosA=sinAcosB，
∴sinBcosA-sinAcosB=0，即sin（A-B）=0，
∵A、B为三角形的两内角，∴A=B，
∴三角形为等腰三角形．
故选：A．

点评本题考查三角形形状的判定，涉及正弦定理和和差角的三角函数公式，属基础题．

练习册系列答案

相关题目

18．

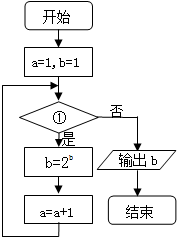已知流程图如图所示，该程序运行后，为使输出的b值为16，则循环体的判断框内①处应填（　　）

19．满足cos（α+β）=cosα+cosβ的α，β的一组值是$\left\{\begin{array}{l}α=\frac{π}{2}\\ β=-\frac{π}{4}.\end{array}\right.$．（写出一组值即可）

16．${∫}_{0}^{2}$（x+1）dx=4．

3．正方体的表面积为24，则该正方体的内切球的体积为$\frac{4π}{3}$．

13．在复平面内，复数z=2+i对应的点在（　　）

20．八人分乘三辆小车，每辆小车至少载1人最多载4人，不同坐法共有（　　）

17．冶炼某种金属可以用旧设备和改造后的新设备，为了检验用这两种设备生产的产品中所含杂质的关系，调查结果如下表所示．

	杂质高	杂质低
旧设备	37	121
新设备	22	202

根据以上数据，则（　　）

	A．	含杂质的高低与设备改造有关		B．	含杂质的高低与设备改造无关
	C．	设备是否改造决定含杂质的高低		D．	以上答案都不对

16．在△ABC中，角A，B，C的对边分别为a，b，c，c=2acosB，则△ABC的形状为等腰三角形．

试题分类