题目内容
16.${∫}_{0}^{2}$(x+1)dx=4.分析 根据定积分的计算法则计算即可.
解答 解:${∫}_{0}^{2}$(x+1)dx=($\frac{1}{2}$x2+x)|${\;}_{0}^{2}$=2+2=4,
故答案为:4.
点评 本题考查了定积分的计算,关键是求出原函数,属于基础题.

练习册系列答案
相关题目
7.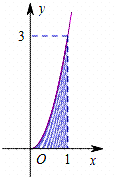 已知函数f(x)的部分图象如图所示.向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为33,由此可估计${∫}_{0}^{1}$f(x)dx的值约为( )
已知函数f(x)的部分图象如图所示.向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为33,由此可估计${∫}_{0}^{1}$f(x)dx的值约为( )
 已知函数f(x)的部分图象如图所示.向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为33,由此可估计${∫}_{0}^{1}$f(x)dx的值约为( )
已知函数f(x)的部分图象如图所示.向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为33,由此可估计${∫}_{0}^{1}$f(x)dx的值约为( )| A. | $\frac{99}{100}$ | B. | $\frac{3}{10}$ | C. | $\frac{9}{10}$ | D. | $\frac{10}{11}$ |
4.在空间直角坐标系O-xyz,点P(1,2,3)关于xOy平面的对称点是( )
| A. | (-1,2,3) | B. | (-1,-2,3) | C. | (1,2,-3) | D. | (1,-2,-3) |
8.已知关于x的方程x2-(bcosA)x+acosB=0的两根之积等于两根之和,且边a,b为△ABC的两内角A,B所对的边,则△ABC是( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
5.若数列{an}的通项公式是an=2×(-3)n,则该数列是( )
| A. | 公比为-3的等比数列 | B. | 公比为2的等比数列 | ||
| C. | 公比为3的等比数列 | D. | 首项为2的等比数列 |
4.若$a={log_{\frac{1}{3}}}2,b={2^{\frac{1}{3}}},c={(\frac{1}{3})^{-\frac{1}{2}}}$,则( )
| A. | a<b<c | B. | b<c<a | C. | c<a<b | D. | c<b<a |