题目内容
19.满足cos(α+β)=cosα+cosβ的α,β的一组值是$\left\{\begin{array}{l}α=\frac{π}{2}\\ β=-\frac{π}{4}.\end{array}\right.$.(写出一组值即可)分析 取特殊值α=$\frac{π}{2}$,β=-$\frac{π}{4}$,验证可得.
解答 解:一般情况下不满足cos(α+β)=cosα+cosβ,
但在特殊情况下是成立的,如α=$\frac{π}{2}$,β=-$\frac{π}{4}$时,
左边=cos$\frac{π}{4}$=$\frac{\sqrt{2}}{2}$,右边=cos(-$\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$
故答案为:$\left\{\begin{array}{l}α=\frac{π}{2}\\ β=-\frac{π}{4}.\end{array}\right.$
点评 本题考查两角和与差的三角函数公式,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.阅读如图所示的程序框图,若输入的k=10,则该算法的功能是( )
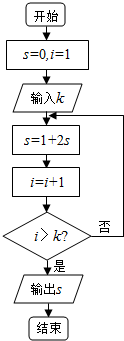

| A. | 计算1+21+22+…+210的和 | B. | 计算1+21+22+…+29的和 | ||
| C. | 计算1+3+7+…+(29-1)的和 | D. | 计算1+3+7+…+(210-1)的和 |
7.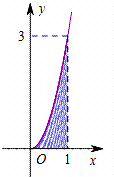 已知函数f(x)的部分图象如图所示.向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为33,由此可估计${∫}_{0}^{1}$f(x)dx的值约为( )
已知函数f(x)的部分图象如图所示.向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为33,由此可估计${∫}_{0}^{1}$f(x)dx的值约为( )
 已知函数f(x)的部分图象如图所示.向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为33,由此可估计${∫}_{0}^{1}$f(x)dx的值约为( )
已知函数f(x)的部分图象如图所示.向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为33,由此可估计${∫}_{0}^{1}$f(x)dx的值约为( )| A. | $\frac{99}{100}$ | B. | $\frac{3}{10}$ | C. | $\frac{9}{10}$ | D. | $\frac{10}{11}$ |
14.如图表示的是求首项为-41,公差为2的等差数列{an}前n项和的最小值的程序框图.则①处可填写( )


| A. | S>0 | B. | S<0 | C. | a>0 | D. | a=0 |
4.在空间直角坐标系O-xyz,点P(1,2,3)关于xOy平面的对称点是( )
| A. | (-1,2,3) | B. | (-1,-2,3) | C. | (1,2,-3) | D. | (1,-2,-3) |
8.已知关于x的方程x2-(bcosA)x+acosB=0的两根之积等于两根之和,且边a,b为△ABC的两内角A,B所对的边,则△ABC是( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
7.已知命题p:?x∈R,2x<3x;命题q:?x∈R,使得log0.5x=x,则下列命题中为真命题的是( )
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |