题目内容

17．冶炼某种金属可以用旧设备和改造后的新设备，为了检验用这两种设备生产的产品中所含杂质的关系，调查结果如下表所示．
杂质高杂质低
旧设备37121
新设备22202
根据以上数据，则（　　）
A．含杂质的高低与设备改造有关B．含杂质的高低与设备改造无关
C．设备是否改造决定含杂质的高低D．以上答案都不对

分析 根据所给的数据写出列联表，把列联表的数据代入观测值的公式，求出两个变量之间的观测值，把观测值同临界值表中的数据进行比较，得到有99%的把握认为含杂质的高低与设备是否改造是有关的．

解答 解：由已知数据得到如下2×2列联表

杂质高杂质低合计
旧设备37121158
新设备22202224
合计59323382
由公式κ2=$\frac{382×（37×202-22×121）^{2}}{59×224×59×323}$≈13.11，
由于13.11＞6.635，故有99%的把握认为含杂质的高低与设备是否改造是有关的．

点评 本题考查独立性检验，考查写出列联表，这是一个基础题．

练习册系列答案
相关题目
7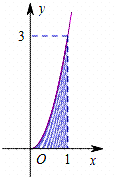．已知函数f（x）的部分图象如图所示．向图中的矩形区域随机投出100粒豆子，记下落入阴影区域的豆子数．通过10次这样的试验，算得落入阴影区域的豆子的平均数约为33，由此可估计${∫}_{0}^{1}$f（x）dx的值约为（　　）
A．$\frac{99}{100}$B．$\frac{3}{10}$C．$\frac{9}{10}$D．$\frac{10}{11}$
8．已知关于x的方程x2-（bcosA）x+acosB=0的两根之积等于两根之和，且边a，b为△ABC的两内角A，B所对的边，则△ABC是（　　）
A．等腰三角形B．等边三角形C．直角三角形D．等腰直角三角形
5．若数列{an}的通项公式是an=2×（-3）n，则该数列是（　　）
A．公比为-3的等比数列B．公比为2的等比数列
C．公比为3的等比数列D．首项为2的等比数列
12．已知 {an}，{bn}均为等差数列，前n项和分别为 Sn，Tn．
（1）若对 n∈N*，有 $\frac{S_n}{T_n}=\frac{31n+101}{n+3}$，求 $\frac{a_n}{b_n}$的最大值．
（2）若平面内三个不共线向量 $\overrightarrow{OA}，\overrightarrow{OB}，\overrightarrow{OC}$满足 $\overrightarrow{OC}={a_3}\overrightarrow{OA}+{a_{15}}\overrightarrow{OB}$，且A，B，C三点共线．是否存在正整数n，使 Sn为定值？若存在，请求出此定值；若不存在，请说明理由．
2．如图，已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的离心率为$\frac{{\sqrt{2}}}{2}$，短轴端点在圆O：x2+y2=1上
（1）求椭圆C的标准方程
（2）设过点A（0，2）的动直线l与圆O有公共点，且与椭圆C相交于P，Q两点，求△OPQ面积的最大值及取得最大值时l的方程．
7．已知命题p：?x∈R，2x＜3x；命题q：?x∈R，使得log0.5x=x，则下列命题中为真命题的是（　　）
A．p∧qB．￢p∧qC．p∧￢qD．￢p∧￢q
4．若$a={log_{\frac{1}{3}}}2，b={2^{\frac{1}{3}}}，c={（\frac{1}{3}）^{-\frac{1}{2}}}$，则（　　）
A．a＜b＜cB．b＜c＜aC．c＜a＜bD．c＜b＜a
5．已知a=2+$\sqrt{3}$，b=1+$\sqrt{6}$，c=$\sqrt{2}$+$\sqrt{5}$，则a，b，c的大小关系为（　　）
A．a＞b＞cB．c＞a＞bC．a＞c＞bD．c＞b＞a

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网