题目内容

20．八人分乘三辆小车，每辆小车至少载1人最多载4人，不同坐法共有（　　）
A．770种B．1260种C．4620种D．2940种

分析 先分组，求出分组的种数，注意平均分组和不平均分组，再分配，根据分步计数原理可得．

解答 解：第一步分步：由题意把8人分为以下三组（1，3，4），（2，2，4），（2，3，3），
分组的种数为C81C73+$\frac{{C}_{8}^{4}•{C}_{4}^{2}}{{A}_{2}^{2}}$+$\frac{{C}_{8}^{2}•{C}_{6}^{3}}{{A}_{2}^{2}}$=280+210+280=770种，
第二步，分配，每一种分法都有A33=6种，
根据分步计数原理，共有770×6=4620种，
故选：C．

点评 本题考查排列组合的实际应用，考查了分组分配的问题，关键是分组是平均分组还是不平均分组，属于中档题．

练习册系列答案
相关题目
10．阅读如图所示的程序框图，若输入的k=10，则该算法的功能是（　　）
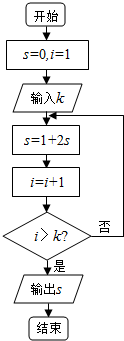
A．计算1+21+22+…+210的和B．计算1+21+22+…+29的和
C．计算1+3+7+…+（29-1）的和D．计算1+3+7+…+（210-1）的和
11．计算${∫}_{-\frac{π}{2}}^{\frac{π}{2}}$（sinx+x）dx=0．
8．已知关于x的方程x2-（bcosA）x+acosB=0的两根之积等于两根之和，且边a，b为△ABC的两内角A，B所对的边，则△ABC是（　　）
A．等腰三角形B．等边三角形C．直角三角形D．等腰直角三角形
15．已知函数f（x）=ex-e-x（e=2.71828…）是自然对数的底数），f（x）的导数是（　　）
A．偶函数B．奇函数C．增函数D．减函数
5．若数列{an}的通项公式是an=2×（-3）n，则该数列是（　　）
A．公比为-3的等比数列B．公比为2的等比数列
C．公比为3的等比数列D．首项为2的等比数列
12．已知 {an}，{bn}均为等差数列，前n项和分别为 Sn，Tn．
（1）若对 n∈N*，有 $\frac{S_n}{T_n}=\frac{31n+101}{n+3}$，求 $\frac{a_n}{b_n}$的最大值．
（2）若平面内三个不共线向量 $\overrightarrow{OA}，\overrightarrow{OB}，\overrightarrow{OC}$满足 $\overrightarrow{OC}={a_3}\overrightarrow{OA}+{a_{15}}\overrightarrow{OB}$，且A，B，C三点共线．是否存在正整数n，使 Sn为定值？若存在，请求出此定值；若不存在，请说明理由．
7．已知命题p：?x∈R，2x＜3x；命题q：?x∈R，使得log0.5x=x，则下列命题中为真命题的是（　　）
A．p∧qB．￢p∧qC．p∧￢qD．￢p∧￢q
8．已知$\overrightarrow{a}$=（cosx，sinx），$\overrightarrow{b}$=（cosx，$\sqrt{3}$cosx），f（x）=2$\overrightarrow{a}$•$\overrightarrow{b}$+1．
（1）求当$x∈[0，\frac{π}{2}]$时，f（x）的值域；
（2）若对任意$x∈[0，\frac{π}{2}]$和任意$α∈[\frac{π}{12}，\frac{π}{3}]$，$k•\sqrt{1+sin2α}-sin2α≤f（x）+1$恒成立，求实数k的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网