题目内容
【题目】已知函数![]() .
.
(1)若函数![]() 与
与![]() 的图象上存在关于原点对称的点,求实数
的图象上存在关于原点对称的点,求实数![]() 的取值范围;
的取值范围;
(2)设![]() ,已知
,已知![]() 在
在![]() 上存在两个极值点
上存在两个极值点![]() ,且
,且![]() ,求证:
,求证:![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)函数![]() 关于原点对称的函数解析式为
关于原点对称的函数解析式为![]() .函数
.函数![]() 与
与![]() 的图象上存在关于原点对称的点,等价于方程
的图象上存在关于原点对称的点,等价于方程![]() 在
在![]() 有解.
有解.
即![]() ,
,![]() ,令
,令![]() ,
,![]() ,利用导数研究函数的单调性极值即可得出.
,利用导数研究函数的单调性极值即可得出.
![]() 等价于
等价于![]() 等价于
等价于![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,再利用导数研究函数的单调性、极值,利用分析法即可得证.
,再利用导数研究函数的单调性、极值,利用分析法即可得证.
(1)函数![]() 与
与![]() 的图像上存在关于原点对称的点,
的图像上存在关于原点对称的点,
即![]() 的图像与函数
的图像与函数![]() 的图像有交点,
的图像有交点,
即![]() 在
在![]() 上有解.
上有解.
即![]() 在
在![]() 上有解.
上有解.
设![]() ,(
,(![]() ),则
),则![]()
当![]() 时,
时,![]() 为减函数;当
为减函数;当![]() 时,
时,![]() 为增函数,
为增函数,
所以![]() ,即
,即![]() .
.
(2)![]() ,
,![]()
![]() 在
在![]() 上存在两个极值点
上存在两个极值点![]() ,
,![]() ,且
,且![]() ,
,
所以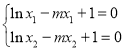
因为![]() 且
且![]() ,所以
,所以![]() ,
,
即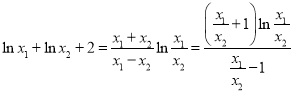
设![]() ,则
,则![]()
要证![]() ,即证
,即证![]() ,
,
只需证![]() ,即证
,即证![]()
设![]() ,
,![]() ,
,
则![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,
即![]()
所以,![]() 即
即![]() .
.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
【题目】下面有三个游戏规则,袋子中分别装有球,从袋中无放回地取球,问其中不公平的游戏是( )
游戏1 | 游戏2 | 游戏3 |
袋中装有一个红球和一个白球 | 袋中装有2个红球和2个白球 | 袋中装有3个红球和1个白球 |
取1个球, | 取1个球,再取1个球 | 取1个球,再取1个球 |
取出的球是红球→甲胜 | 取出的两个球同色→甲胜 | 取出的两个球同色→甲胜 |
取出的球是白球→乙胜 | 取出的两个球不同色→乙胜 | 取出的两个球不同色→乙胜 |
A.游戏1B.游戏2C.游戏3D.游戏2和游戏3
【题目】华为公司在2017年8月9日推出的一款手机,已于9月19日正式上市.据统计发现该产品的广告费用x与销售额y的统计数据如下表:
广告费用x(百万元) | 4 | 2 | 3 | 5 |
销售额y(百万元) | 44 | 25 | 37 | 54 |
根据上表可得回归方程![]() 中的
中的![]() 为9.4,据此模型预测广告费用为6百万元时,销售额为( )
为9.4,据此模型预测广告费用为6百万元时,销售额为( )
A.61.5百万元B.62.5百万元C.63.5百万元D.65.0百万元