题目内容
【题目】某种零件的质量指标值以分数(满分100分)衡量,并根据分数的高低划分三个等级,如下表:

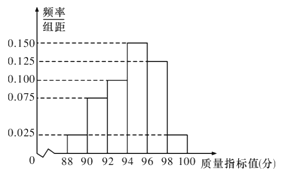
为了监控某种零件的一条生产线的生产过程,检验员随机抽取了100件零件,进行质量指标值检查,将检查结果进行整理得到如下的频率分布直方图:
(1)若该生产线的质量指标值要求为:
第一条:生产线的质量指标值合格和优秀的零件至少要占全部零件的75%,
第二条:生产线的质量指标值平均分不低于95分;
如果同时满足以上两条就认定生产线的质量指标值合格,否则为不合格,请根据以上抽样调查数据,判断该生产线的质量指标值是否合格?
(2)在样本中,按质量指标值的等级用分层抽样的方法从质量指标值不合格和优秀的零件中抽取5件,再从这5件中随机抽取2件,求这两件的质量指标值恰好一个不合格一个优秀的概率
【答案】(1)可以判断该生产线的质量指标值是不合格的,详见解析(2)![]()
【解析】
(1)根据频率分布直方图,计算出生产线的质量指标值合格和优秀的零件所占比例的估计值和生产线的质量指标值平均分,然后进行判断;(2)先利用分层抽样的特点,得到所抽取出的5件零件中不合格和优秀的数量,然后将5件中随机抽取2件的情况全部列出,根据古典概型的公式,得到答案.
(1)根据抽样调查数据,生产线的质量指标值合格和优秀的零件所占比例的估计值为:
(0.100+0.150+0.125+0.025)×2=0.80,
因为0.80>0.75,所以满足生产线质量指标值要求的第一条;
生产线的质量指标值平均分约为:
(89×0.025+91×0.075+93×0.100+95×0.150+97×0.125+99×0.025)×2=94.4,
因为94.4<95,所以不满足生产线质量指标值要求的第二条;
综上,可以判断该生产线的质量指标值是不合格的.
(2)由频率分布直方图可知,不合格、优秀的频率分别为0.2,0.3,
故在样本中用分层抽样方法从质量指标值不合格和优秀的零件中抽取5件零件,质量指标值不合格的有2件,设为甲、乙,优秀的有3件,设为A,B,C。从这5件零件中随机抽取2件,有:
甲乙,甲A,甲B,甲C,乙A,乙B,乙C,AB,AC,BC,共10种,
其中恰好一个不合格一个优秀的有:甲A,甲B,甲C,乙A,乙B,乙C共6种
所以这两件的质量指标值恰好一个不合格一个优秀的概率P=![]()
