题目内容
【题目】在正方体ABCD﹣A1B1C1D1中，下列判断正确的是（ ）
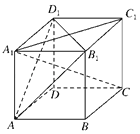
A.A1C⊥面AB1D1B.A1C⊥面AB1C1D
C.A1B⊥面AB1D1D.A1B⊥AD1
【答案】A
【解析】
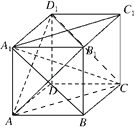
由已知证明A1C⊥B1D1，A1C⊥AB1，得A1C⊥平面AB1D1，说明A正确，B不正确，再求出A1B与AD1 所成角为60°，说明C，D错误．
解：在正方体ABCD﹣A1B1C1D1中，A1C1⊥B1D1，
又CC1⊥B1D1，且A1C1∩CC1＝C1，∴B1D1⊥平面A1C1C，则A1C⊥B1D1，
同理A1C⊥AB1，则A1C⊥平面AB1D1，故A正确，B不正确；
连接D1C，AC，则∠AD1C为A1B与AD1 所成角，为60°，故C、D不正确．
故选：A．
练习册系列答案
相关题目
