题目内容
(本小题满分14分)
设函数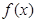 对任意实数
对任意实数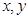 都有
都有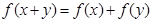 且
且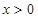 时
时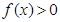 。
。
(Ⅰ)证明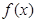 是奇函数;
是奇函数;
(Ⅱ)证明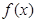 在
在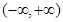 内是增函数;
内是增函数;
(Ⅲ)若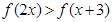 ,试求
,试求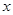 的取值范围。
的取值范围。
设函数
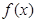 对任意实数
对任意实数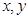 都有
都有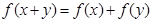 且
且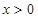 时
时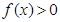 。
。(Ⅰ)证明
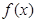 是奇函数;
是奇函数;(Ⅱ)证明
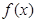 在
在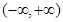 内是增函数;
内是增函数;(Ⅲ)若
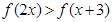 ,试求
,试求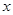 的取值范围。
的取值范围。(Ⅰ)证明: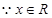 ,
,
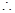 函数
函数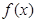 的定义域关于原点对称,
的定义域关于原点对称,
令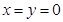 ,则
,则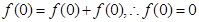 ,
,
令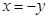 ,则
,则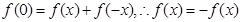 ,
,
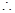 函数
函数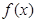 为奇函数。(4分)
为奇函数。(4分)
(Ⅱ)证明:设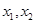 是
是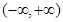 内任意两实数,且
内任意两实数,且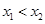 ,则
,则
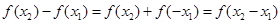 ,
,
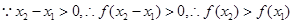 ,
,
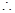 函数
函数 在
在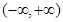 内是增函数。(4分)
内是增函数。(4分)
(Ⅲ)解: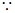 函数
函数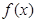 在
在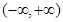 内是增函数,且
内是增函数,且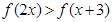 ,
,
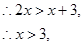
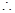
 的取值范围为
的取值范围为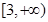 。(4分)
。(4分)
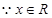 ,
, 函数
函数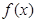 的定义域关于原点对称,
的定义域关于原点对称,令
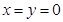 ,则
,则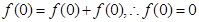 ,
,令
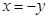 ,则
,则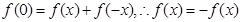 ,
,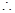 函数
函数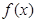 为奇函数。(4分)
为奇函数。(4分)(Ⅱ)证明:设
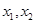 是
是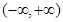 内任意两实数,且
内任意两实数,且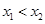 ,则
,则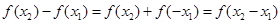 ,
,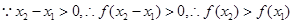 ,
,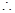 函数
函数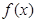 在
在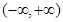 内是增函数。(4分)
内是增函数。(4分)(Ⅲ)解:
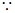 函数
函数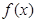 在
在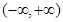 内是增函数,且
内是增函数,且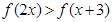 ,
,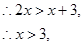
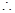
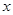 的取值范围为
的取值范围为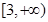 。(4分)
。(4分)略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
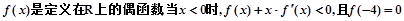 ,则不等式
,则不等式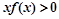 的解集为( )
的解集为( )



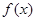 是定义在
是定义在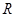 上的奇函数,当
上的奇函数,当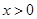 时,
时,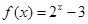 ,那么
,那么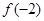 的值是( )
的值是( )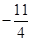
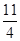
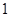
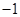
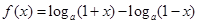
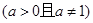
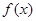 的奇偶性与单调性;
的奇偶性与单调性;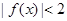 的解集为
的解集为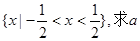 的值;
的值;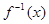 ,若关于
,若关于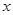 的不等式
的不等式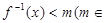 R)有解,求
R)有解,求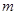 的取值范围.
的取值范围.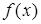 是定义在
是定义在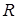 上的偶函数,对任意
上的偶函数,对任意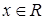 ,都有
,都有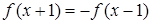 ,且当
,且当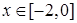 时,
时,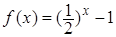 ,若在区间
,若在区间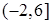 内关于
内关于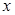 的方程
的方程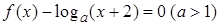 恰有3个不同的实数根,则
恰有3个不同的实数根,则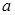 的取值范围是( )
的取值范围是( )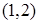
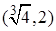
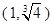
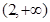
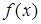 为奇函数, 且在(-∞, 0)内是减函数, f(-2)=" 0," 则
为奇函数, 且在(-∞, 0)内是减函数, f(-2)=" 0," 则 的解集为 ( )
的解集为 ( ) 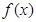 是定义在
是定义在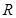 上的奇函数,当
上的奇函数,当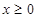 时,
时,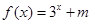 (
(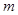 为常数),则
为常数),则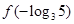 的值为
的值为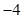
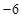
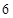
 ,若
,若 ,则
,则 。
。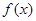 是定义在R上的奇函数,当
是定义在R上的奇函数,当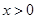 时,
时,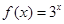 ,则
,则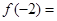 ______。
______。