题目内容
已知p:|1-
|≤2,q:x2-2x+1-m2≤0(m>0).若“非p”是“非q”的必要而不充分条件,求实数m的取值范围.
| x-1 |
| 3 |
解法一:由p:|1-
|≤2,解得-2≤x≤10,
∴“非p”:A={x|x>10或x<-2}、(3分)
由q:x2-2x+1-m2≤0,解得1-m≤x≤1+m(m>0)
∴“非q”:B={x|x>1+m或x<1-m,m>0=(6分)
由“非p”是“非q”的必要而不充分条件可知:B⊆A.
解得m≥9.
∴满足条件的m的取值范围为{m|m≥9}.(12分)
解法二:由“非p”是“非q”的必要而不充分条件.即“非q”⇒“非p”,但“非p”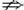 “非q”,可以等价转换为它的逆否命题:“p⇒q,但q
“非q”,可以等价转换为它的逆否命题:“p⇒q,但q p”.即p是q的充分而不必要条件.
p”.即p是q的充分而不必要条件.
由|1-
|≤2,解得-2≤x≤10,
∴p={x|-2≤x≤10}
由x2-2x+1-m2≤0,解得1-m≤x≤1+m(m>0)
∴q={x|1-m≤x≤1+m,m>0}
由p是q的充分而不必要条件可知:
p⊆q?
解得m≥9.
∴满足条件的m的取值范围为{m|m≥9}.
| x-1 |
| 3 |
∴“非p”:A={x|x>10或x<-2}、(3分)
由q:x2-2x+1-m2≤0,解得1-m≤x≤1+m(m>0)
∴“非q”:B={x|x>1+m或x<1-m,m>0=(6分)
由“非p”是“非q”的必要而不充分条件可知:B⊆A.
|
∴满足条件的m的取值范围为{m|m≥9}.(12分)
解法二:由“非p”是“非q”的必要而不充分条件.即“非q”⇒“非p”,但“非p”
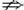 “非q”,可以等价转换为它的逆否命题:“p⇒q,但q
“非q”,可以等价转换为它的逆否命题:“p⇒q,但q p”.即p是q的充分而不必要条件.
p”.即p是q的充分而不必要条件.由|1-
| x-1 |
| 3 |
∴p={x|-2≤x≤10}
由x2-2x+1-m2≤0,解得1-m≤x≤1+m(m>0)
∴q={x|1-m≤x≤1+m,m>0}
由p是q的充分而不必要条件可知:
p⊆q?
|
∴满足条件的m的取值范围为{m|m≥9}.

练习册系列答案
相关题目